SOLUTION: what is the exact value of csc(tan-1(7x))

That asks the question:



So first we draw a right triangle containing an angle θ



Now let's make sure that the tangent of θ is 7x.  To do that
we remember that .
Now we write 7x as the fraction 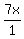, label the OPPOSITE side
of θ as the NUMERATOR of that fraction, which is 7x, and label the 
ADJACENT side of θ as the DENOMINATOR of that fraction, which is 1.
We also find the hypotenuse of the right triangle by the Pythagorean 
theorem: 





and label the hypotenuse as that:



Now the problem asks:

If the tangent of an angle is 7x, what is its cosecant?

We remember that .

So the cosecant is .

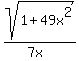If x is positive, 7x will be positive.
The tangent is positive in QI and QIII.
The cosecant is positive in QI and negative in QIII.

Is x is negative, 7x will be negative
The tangent is negative in QII and QIV
the cosecant is positive in QII and negative in QIV.

Therefore to be sure to give all possible answers, and not just cases
where x is positive and θ is in QI, we must put ± before
the final answer:

Answer:  .

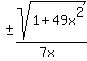Edwin