|
Question 97177: After 5 hours of painting, Jess asked the for assistance of Jon.Together, they finished the job in 4 more hours.If Jon had joined in an hour after Jess started working, the job would have been finished in 7 hours. How long would it have taken for Jess to paint the house alone?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! After 5 hours of painting, Jess asked the for assistance of Jon. Together, they finished the job in 4 more hours.If Jon had joined in an hour after Jess started working, the job would have been finished in 7 hours. How long would it have taken for Jess to paint the house alone?
:
Let the completed job = 1
:
Let x = time if Jess did the job alone
:
Let y = time if Jon did the job alone
:
We know that after 5 hrs, he would complete 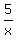 of the job of the job
:
Jess alone for 5 hr, together with Jon for 4 hrs, (a total of 9 hrs)
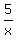 + +  + + 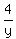 = 1 = 1
:
5y + 4y + 4x = xy
:
9y + 4x = xy
:
Jess alone for 1 hr, together for 6 hr (a total of 7 hrs)
 + +  + + 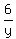 = 1 = 1
:
y + 6y + 6x = xy
:
7y + 6x = xy
:
Since both equations = xy, make them equal to each other
9y + 4x = 7y + 6x
9y - 7y = 6x - 4x
2y = 2x
y = x
:
Rewrite the initial work equation substituting x for y
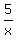 + +  + + 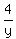 = 1 = 1
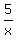 + +  + +  = 1 = 1
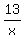 = 1 = 1
Therefore x = 13 hrs for Jess to do it alone
:
The same time would be required by Jon (y), prove that in the 2nd work equation
Substitute 13 for x in the 2nd work equation, solve for y:
 + +  + + 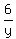 = 1 = 1
 + + 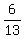 + + 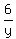 = 1 = 1
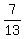 + + 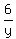 = 1 = 1
7y + 13(6) = 13y
78 = 13y - 7y
6y = 78
y = 13 hr, Jon alone also
:
Did this help? Make any sense to you?
|
|
|
| |