what is the smallest of 3 consecutive positive integers if the product of the
smaller two integers is 11 more than 5 times the largest integer
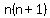

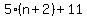
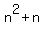

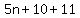
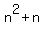

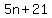 Get 0 on the right side:
Get 0 on the right side:


 Factor the left side:
Factor the left side:
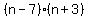

 Set each factor = 0
n-7 = 0; n+3 = 0
n = 7; n = -3
Since the problem specifically states "positive":
we ignore the negative answer.
Answer: 7,8,9
Checking product of smaller two = 7*8 = 56
5 times the largest = 5*9 = 45
11 more than 45 is 56.
So the solution 7,8,9 is correct.
Edwin
Set each factor = 0
n-7 = 0; n+3 = 0
n = 7; n = -3
Since the problem specifically states "positive":
we ignore the negative answer.
Answer: 7,8,9
Checking product of smaller two = 7*8 = 56
5 times the largest = 5*9 = 45
11 more than 45 is 56.
So the solution 7,8,9 is correct.
Edwin