Question 970876: a (5;5);(-7;1); and c (1;-7) are the vertices of triangle ABC.show that ABC is an isosceles triangle.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! a ( , ,  ); b ( ); b ( , , ); and c ( ); and c ( , , ) are the vertices of triangle ABC ) are the vertices of triangle ABC
to show that ABC is an 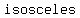 triangle, we need to show that the distance between two vertices is triangle, we need to show that the distance between two vertices is 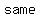 ; so, use the distance formula ; so, use the distance formula
the distance between  and and 
a ( , ,  ); );
b ( , , ) )






or

the distance between  and and 
a ( , ,  ); );
c ( , , ) )






or

as you can see,  => so, ABC is an => so, ABC is an 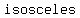 triangle triangle
let's draw it too
first find equation of a line through each two points:
a line through points  and and 
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (5, 5) and (x2, y2) = (-7, 1).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(0.333333333333333)x + (3.33333333333333)
Your graph:

|
a line through points  and and 
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (5, 5) and (x2, y2) = (1, -7).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(3)x + (-10)
Your graph:

|
a line through points  and and 
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (-7, 1) and (x2, y2) = (1, -7).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(-1)x + (-6)
Your graph:

|
so, equations are:



graph all together:

|
|
|