Question 969969: Calculate the volume of a cone shaped pare cup that can be folded from a circle sector. Give your answer correct to 1 decimal point.. I have no idea how to calculate the height and radius.
Circle sector - radius equals to 8cm
Angle measure- 90 degrees.
Answer by josgarithmetic(39625)   (Show Source):
You can put this solution on YOUR website! Managing this in a visualization all in the head, slant height remains 8 cm, circumference of the base is 2 cm, and then you can find the radius of the circular base. From that, you should be able to calculate the height or distance from cone tip to the center of the circular base.
h, tip-to-center height
r, radius
-
 , being reminded that 8 cm is the slant height, and we use the Pythagorean theorem relationship. Use this to find the value of h.
-
volume for the cone is  .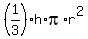
"Visualizing all in the head" is one way to know what is happening, but you have your description, and from that, you can draw and create a physical model. Bend the sector to make the two radii meet. That will be your cone. The height, slant height, and radius form a right triangle. Slant height is hypotenuse, and the base radius and cone height are the legs. Use Pythagorean Theorem to find the height. You already know the radius of the original sector, and when you form the cone, that radius becomes the slant height of the cone; which is now the hypotenuse of the right triangle.
8 is radius of the original sector.
This sector of 90 degree, has an arc  .
In other words, the radius of the cone's base is  .
-
You want to know the height of the cone.
Radius of base, .
Hypotenuse same as slant height, 8 cm.
If height is h, then  . You can find value of h from this.
|
|
|
