When you see "arc" in front of "sin", that is to be read as
"Angle whose sine is".
When you see "arc" in front of "cos", that is to be read as
"Angle whose cosine is"
When you see "arc" in front of "tan", that is to be read as
"Angle whose tangent is"
And so forth with arcsec, arccsc, and arcot.
Since the sine of 30° is 1/2, then arcsin(1/2) is 30°.
But the sine 135° is also 1/2, so why isn't the arcsin(1/2)
equal to 150° also?
Answer: Because the mathematicians of old wanted the inverse sine
to be a function and have only one output for each input, so they
said "Let us restrict the values of arcsin(x) and arctan(x) to only
between  and
and 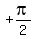 or -90° to 90°, inclusive
for arcsine and exclusive for arctangent.
------------
or -90° to 90°, inclusive
for arcsine and exclusive for arctangent.
------------
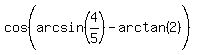
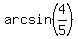 means the angle whose sine is
means the angle whose sine is  .
.
 Instead of calculating it, we will draw that angle. Since the
sine is
Instead of calculating it, we will draw that angle. Since the
sine is 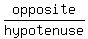 we draw a right triangle that
1. has the numerator of
we draw a right triangle that
1. has the numerator of  , which is 4, on the opposite
side, and
2. has the denominator or
, which is 4, on the opposite
side, and
2. has the denominator or  , which is 5, on the hypotenuse.
We can now find the side adjacent to a by the Pythagorean theorem:
, which is 5, on the hypotenuse.
We can now find the side adjacent to a by the Pythagorean theorem:






 ---
---
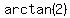 means the angle whose tangent is
means the angle whose tangent is  or
or 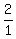 .
.
 Instead of calculating it, we will draw that angle. Since the
tangent is
Instead of calculating it, we will draw that angle. Since the
tangent is 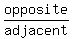 we draw a right triangle that
1. has the numerator of
we draw a right triangle that
1. has the numerator of 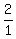 , which is 2, on the opposite
side and
2. has the denominator of
, which is 2, on the opposite
side and
2. has the denominator of 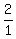 , which is 1, on the side adjacent
to b. We can find the hypotenuse by the Pythagorean theorem:
, which is 1, on the side adjacent
to b. We can find the hypotenuse by the Pythagorean theorem:





 Now that we have those two triangles drawn, we can now do the
problem:
Now that we have those two triangles drawn, we can now do the
problem:
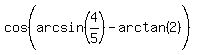

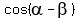

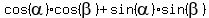 Now we just look at those two triangles and get
Now we just look at those two triangles and get

 (rationalized)
(rationalized)

 (rationalized)
(rationalized)
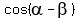

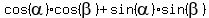
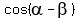

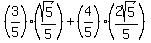
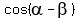

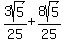
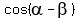

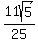 Edwin
Edwin