|
Question 969843: In a two digit number, a new number is formed by reversing the digits and adding
3. The new number is 2 more than double the original number. What is the
original number?
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a two digit number, a new number is formed by reversing the digits and adding
3. The new number is 2 more than double the original number. What is the
original number?
original number = 10t+u
new number = 10u+t+3
10u+t+3 = 2(10t+u)+2
10u+t+3 = 20t+2u+2
8u+1 = 19t
Write 19 in terms of its nearest multiple of the smaller coefficient 8,
as, 16+3
8u+1 = (16+3)t
8u+1 = 16t+3t
Divide through by the smaller coefficient, 8:
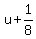  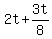 Isolate fractions on
Isolate fractions on
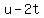  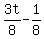 The left side is an integer, therefore so is the right side, say integer A
u-2t=A and
The left side is an integer, therefore so is the right side, say integer A
u-2t=A and  3t-1=8A
Write 8 as 9-1
3t-1=(9-1)A
3t-1=9A-A
Divide through by 3
3t-1=8A
Write 8 as 9-1
3t-1=(9-1)A
3t-1=9A-A
Divide through by 3
 Isolate the fractions:
Isolate the fractions:
 The right side is an integer, therefore so is the left side, say integer B
The right side is an integer, therefore so is the left side, say integer B
 , 3A-t=B
A-1=3B
A=3B+1
3A-t=B
3(3B+1)-t=B
9B+3-t=B
8B+3=t
Since t is a digit, B=0 and t=3
Substitute in:
8u+1 = 19t
8u+1 = 19(3)
8u+1 = 57
8u = 56
u = 7
So the original number is 37.
-----
Checking:
Reversing the digits is 73.
Adding 3 gives 76.
76 is 2 more than 74.
74 is 2 times 37.
So it checks.
Edwin , 3A-t=B
A-1=3B
A=3B+1
3A-t=B
3(3B+1)-t=B
9B+3-t=B
8B+3=t
Since t is a digit, B=0 and t=3
Substitute in:
8u+1 = 19t
8u+1 = 19(3)
8u+1 = 57
8u = 56
u = 7
So the original number is 37.
-----
Checking:
Reversing the digits is 73.
Adding 3 gives 76.
76 is 2 more than 74.
74 is 2 times 37.
So it checks.
Edwin
|
|
|
| |