Although the other tutor got the right answer, she is incorrect
for multiplying both sides of the inequality by the variable x.
That's because a variable x might not be positive, and if you
multiply through by a negative, that would reverse the > to <.
Also she did not use test values on the intervals.
Here is a correct solution:
Solve the following inequality 63x-32>63/x


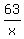 Get 0 on the right side by subtracting
Get 0 on the right side by subtracting 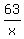 from both sides:
from both sides:
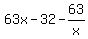

 Get the LCD = x on the left side:
Get the LCD = x on the left side:
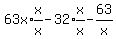


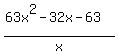

 Factor the numerator on the left:
Factor the numerator on the left:

 We find all the critical numbers. They are the values
obtained by setting the numerator=0 and the denominator=0
The numerator (7x-9)(9x+7) when set equal to 0 gives
critical numbers
We find all the critical numbers. They are the values
obtained by setting the numerator=0 and the denominator=0
The numerator (7x-9)(9x+7) when set equal to 0 gives
critical numbers 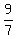 and
and 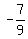 The denominator x when set equal to 0 gives the critical
number 0.
We draw a number line and mark the critical numbers on it,
in order from smallest to largest.
-----o------o--------------------o--------------
-7/9 0 9/7
We have 4 intervals to test by substituting a test point in the interval:
1. Left of
The denominator x when set equal to 0 gives the critical
number 0.
We draw a number line and mark the critical numbers on it,
in order from smallest to largest.
-----o------o--------------------o--------------
-7/9 0 9/7
We have 4 intervals to test by substituting a test point in the interval:
1. Left of 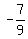 , which is
, which is  2. Between
2. Between 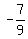 and
and  , which is
, which is 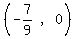 3. Between
3. Between  and
and 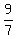 , which is
, which is 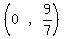 4. Right of
4. Right of 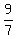 , which is
, which is 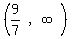 1. The easiest number in
1. The easiest number in  to test in the original is x = -1
to test in the original is x = -1


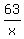
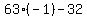

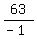
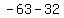

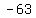
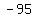

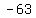 That's false so the solution set does not include
That's false so the solution set does not include  2. The easiest number in
2. The easiest number in 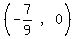 to test in the original is x = -.1
to test in the original is x = -.1


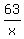
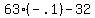

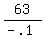
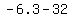

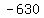
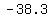

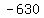 That's true so the solution set does include
That's true so the solution set does include 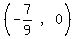 3. The easiest number in
3. The easiest number in 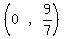 to test in the original is x = 1
to test in the original is x = 1


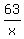
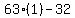

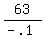


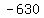
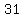

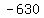 That's true so the solution set does include
That's true so the solution set does include 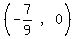 3. The easiest number in
3. The easiest number in 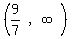 to test in the original is x = 2
to test in the original is x = 2


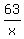
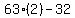

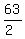
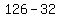

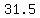
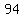

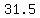 That's true so the solution set does include
That's true so the solution set does include 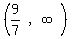 None of the critical numbers are part of the solution since the
symbol is > and not ≥.
So the solution set is:
None of the critical numbers are part of the solution since the
symbol is > and not ≥.
So the solution set is:

a.) Is the point x=0 included in the solution set of the inequality?
No because if we substitute x=0,
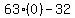

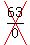 It is meaningless to divide by zero.
It is meaningless to divide by zero.
b.) are the other finite end points of the interval included in the solution set?
No because the symbol is > and not ≥
c.) what is the solution set? (in interval notation)
 Edwin
Edwin