SOLUTION: "Solve the following set of equations using Cramer's rule or matrix inversion for x+5y=7 & -2x-7y=-5"

I'll do it both ways:

By Cramer's rule:



 1x + 5y =  7
-2x - 7y = -5

Form the determinant D which is the
coefficients as they appear left of
the equal sign when in general form:

  

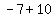
The "column of constants" is 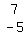, consisting of the numbers
right of the equal signs is not used in the determinant D 
but is used in the other two determinants.

Dx is formed by replacing the FIRST column of D (the 
coefficients of x, the FIRST variable) by the column of constants:



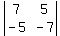
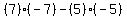
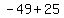
Dy is formed by replacing the SECOND column of D (the 
coefficients of y, the SECOND variable) by the column of constants:


 

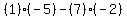
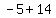
Then:



   

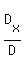
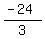
So we see that x = -8 and y = 3

The solution is (x,y) = (-8,3)

---------------------------------------

By matrix inversion:

 1x + 5y =  7
-2x - 7y = -5

Form the matrix equation:



Now we find the inverse of the coefficient matrix 

To find the inverse of a 2x2 matrix: 

1. find the determinant of the matrix:
=

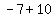
[Note that this is exactly the same as the determinant D in Cramer's rule
above.]

2. Swap the upper left and lower right elements:


3. Change the signs of the upper right and lower left elements:


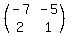4. Divide every term by the value of the determinant in step 1, which is 3.


Now go back to the matrix equation


            
Multiply the inverse matrix on the left of the
left side and also on the left of the right side;



I assume you know how to multiply matrices. If you
don't, post again asking how to. Multiply the first
two matrices on the left, and multiply the matrices on
the right:

            

We have the identity matrix on the left to multiply by
the matrix 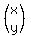 which just gives:

                

So we see that x = -8 and y = 3.

The solution is (x,y) = (-8,3)

Edwin