Question 968758: Please help, I posted this question earlier only to realise I had put 1π instead of 1/2π like i should have.
Consider the trigonometric function f (t) = −1 + 4 sin( 1/2 π(t − 1)).
(a) What is the amplitude of f(t)? (b) What is the period of f(t)?
(c) What are the maximum and minimum values attained by f(t)? (d) Sketch the graph of f (t) for t ∈ [−1, 3].
Found 2 solutions by Edwin McCravy, Theo:
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(t) = −1 + 4 sin( 1/2 π(t − 1)).
Rule:
For 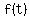  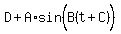 1. The amplitude is |A|
2. The period is
1. The amplitude is |A|
2. The period is 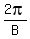 3. The horizontal "phase" shift or displacement is -C.
4. The vertical shift or displacement is D.
5. If A > 0, the maximum value is reached when t is such that
3. The horizontal "phase" shift or displacement is -C.
4. The vertical shift or displacement is D.
5. If A > 0, the maximum value is reached when t is such that  and the minimum value is reached when t is such that
and the minimum value is reached when t is such that  6. If A < 0, the maximum value is reached when t is such that
6. If A < 0, the maximum value is reached when t is such that  and the minimum value is reached when t is such that
and the minimum value is reached when t is such that  For
For 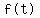  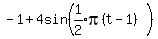 1. The amplitude is |A| = |4| = 4
2. The period is
1. The amplitude is |A| = |4| = 4
2. The period is 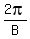     3. The horizontal "phase" shift or displacement is -C = -(-1) = +1
4. The vertical shift or displacement is D = -1
5. If A > 0, the maximum value is reached when t is such that
3. The horizontal "phase" shift or displacement is -C = -(-1) = +1
4. The vertical shift or displacement is D = -1
5. If A > 0, the maximum value is reached when t is such that  Since 4 > 0,
Since 4 > 0, 
 Multiply both sides by
Multiply both sides by 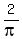

 To find that maximum value we substitute 2 for t in the
original equation:
To find that maximum value we substitute 2 for t in the
original equation:
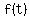  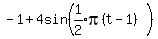
  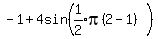
  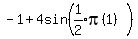
  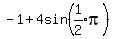
  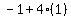
  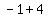
   and the minimum value is reached when t is such that
and the minimum value is reached when t is such that  Since 4 > 0,
Since 4 > 0, 
 Multiply both sides by
Multiply both sides by 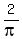

 To find that minimum value we substitute 0 for t in the
original equation:
To find that minimum value we substitute 0 for t in the
original equation:
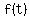  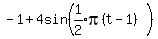
  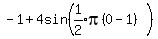
  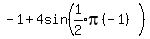
  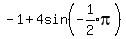
  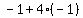
  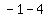
   The graph below shows the maximum value of 3 at t=2, and the
minimum value of -5 at t=0.
The graph below shows the maximum value of 3 at t=2, and the
minimum value of -5 at t=0.
 The green dashed line shows the vertical displacement of -1 below the horizontal
axis. The horizontal shift was actually 1 to the right and to show the basic
shifted period we would have drawn the graph on t∈[1,5] rather than for t∈[−1,3],
but you were instructed to draw the graph on t∈[−1,3]. Then the minimum would
have been reached at t=4 instead of t=0. Notice that we could have used
The green dashed line shows the vertical displacement of -1 below the horizontal
axis. The horizontal shift was actually 1 to the right and to show the basic
shifted period we would have drawn the graph on t∈[1,5] rather than for t∈[−1,3],
but you were instructed to draw the graph on t∈[−1,3]. Then the minimum would
have been reached at t=4 instead of t=0. Notice that we could have used  instead of
instead of  since they are coterminal. That would have given us t=4.
TMI (i.e., Too Much Information, right? J.)
Edwin since they are coterminal. That would have given us t=4.
TMI (i.e., Too Much Information, right? J.)
Edwin
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the general formula for the sine function is:
y = a * sin(b * (x-c)) + d
a is the amplitude
b is the frequency
c is the horizontal shift.
d is the vertical shift.
the normal period of the sine function is 2*pi.
the formula for the period is:
period = (2 * pi) / freqauency.
when a or b or c or d are not shown, their default values are:
a = 1
b = 1
c = 0
d = 0
when d = 0, the center line of the graph is at y = 0.
when d = -1, the center line of the graph is at y = -1.
when b = 1, the period = 2 * pi divided by 1 which is equal to 2 * pi.
your formula brecomes:
f(t) = 4 * sin(pi/2 * x) - 1
your amplitude = 4
your frequency = pi/2
your horizontal shift = 0
your vertical shift = -1
the center line of your graph is at y = -1
the maximum value of your graph is -1 + 4 = 3
the minimum value of your graph is -1 - 4 = -5
your period is equal to 2 * pi divided by pi/2.
this makes your period equal to 5.
your horizontal shift is one unit to the right.
this one is a litle tricky to figure out, so we'll go through a calculation to show you what happens.
your questions were:
a) What is the amplitude of f(t)?
the amplitude is equal to 4
(b) What is the period of f(t)?
the period is 4 radians
(c) What are the maximum and minimum values attained by f(t)?
the maximum value is f(T) = 3
the minimum value is f(t) = -5
(d) Sketch the graph of f (t) for t ∈ [−1, 3].
the graph is shown below:

the period from x = -1 to x = 3 is marked between vertical dashed lines.
the center line of the graph is at y = -1
the maximum value is at y = 3 and the minimum value is at y = -5.
you can see that the graph crosses the center line at x = -1, x = 1, x = 3 and x = 5.
the center line is at y = -1.
take away the vertical displacement of -1 and the center line would have been at the x-axis.
you would analyze this graph as follows:
when x = 3, the equation of the graph becomes:
y = 4 * sin(pi/2 * (3-1)) - 1
this becomes y = 4 * sin(pi/2 * 2) - 1
this becomes y = 4 * sin(pi) - 1
sin(pi) is equal to 0.
the equation becomes y = 4 * 0 - 1
it finally becomes y = -1.
you can see on the graph that, when x = 3, y = -1.
this agrees with the equation.
we'll do one more.
when x = -1, the equation of y = 4 * sin(pi/2 * (x-1)) - 1 becomes:
y = 4 * sin(pi/2 * (-1-1)) - 1 which becomes:
y = 4 * sin(pi/2 * -2) - 1 which becomes:
y = 4 * sin(-pi) - 1 which becomes:
y = 4 * 0 - 1 which becomes:
y = -1.
when x = -1, the value of y is equal to -1.
the graph confirms that.
|
|
|