SOLUTION: Good Morning, Can anyone show me the steps for this, please? Consider the following equation and determine if it is a parabola, an ellipse, or a hyperbola and sketch it's graph:

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Good Morning, Can anyone show me the steps for this, please? Consider the following equation and determine if it is a parabola, an ellipse, or a hyperbola and sketch it's graph:      Log On


   

Question 968175: Good Morning, Can anyone show me the steps for this, please?
Consider the following equation and determine if it is a parabola, an ellipse, or a hyperbola and sketch it's graph:
4y^2+6x-2y+3x^2-15=2y^2+4x^2
Thank you in advance for your help.
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
Consider the following equation and determine if it is a parabola, an ellipse, or a hyperbola and sketch it's graph:
4y^2+6x-2y+3x^2-15=2y^2+4x^2 

4y%5E2%2B6x-2y%2B3x%5E2-15=2y%5E2%2B4x%5E2

Subtract the right side from both sides to get 0 on the right:

2y%5E2%2B6x-2y-x%5E2-15=0

We can tell this is the graph of a hyperbola because the x² and 
y² terms have opposite signs when all non-zero terms are one 
side and all like terms combined. 

Get the y terms together and the x terms together, and add 15
to both sides to get the contant term off the left side:

2y%5E2-2y-x%5E2%2B6x=15

Factor the coefficient of the y² term, which is 2, out of the 
first two terms on the left, skipping a space at the end of the
parentheses.

Factor the coefficient of the x² term, which is -1, out of the 
last two terms on the left, skipping a space at the end of the
parentheses.


  

Complete the square inside each parentheses:

In your head or on scratch paper,
1. Multiply the coefficient of y, which is -1, by 1/2, getting -1/2.
2. Square -1/2, getting (-1/2)² = +1/4
3. Add +1/4 in the space in the first parentheses, which amounts to
   adding 2 times +1/4 or +1/2 to the left side. So add +1/2 to the right 
   side.

1. Multiply the coefficient of x, which is -6, by 1/2, getting -3.
2. Square -3, getting (-3)² = +9
3. Add +9 in the space in the first parentheses, which amounts to
   adding -1 times +9 or -9 to the left side. So add -9 to the 
   right side.

2%28y%5E2-y%2B1%2F4%29-1%28x%5E2-6x%2B9%29=15%2B1%2F2-9

Factor each trinomial: y%5E2-y%2B1%2F4=%28y-1%2F2%29%28y-1%2F2%29=%28y-1%2F2%29%5E2
                       x%5E2-6x%2B9=%28x-3%29%28x-3%29=%28x-3%29%5E2
Combine the terms on the right 15%2B1%2F2-9=6%2B1%2F2=13%2F2

2%28y-1%2F2%29%5E2-1%28x-3%29%5E2=13%2F2

Clear the fraction on the right by multiplying 
through by 2:

4%28y-1%2F2%29%5E2-2%28x-3%29%5E2=13

Get 1 on the right by dividing through by 13:

4%28y-1%2F2%29%5E2%2F13-2%28x-3%29%5E2%2F13=1

Divide numerator and denominator by the coefficients of
the squares of the binomials:

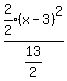
expr%284%2F4%29%28y-1%2F2%29%5E2%2Fexpr%2813%2F4%29%22%22-%22%22expr%282%2F2%29%28x-3%29%5E2%2Fexpr%2813%2F2%29%22%22=%22%221

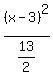%28y-1%2F2%29%5E2%2Fexpr%2813%2F4%29%22%22-%22%22%28x-3%29%5E2%2Fexpr%2813%2F2%29%22%22=%22%221

This is in standard form:

%28y-k%29%5E2%2Fa%5E2-%28x-h%29%5E2%2Fb%5E2=1 which is the equation of a hyperbola which
opens like this:                                  
  
So h=3, k=1%2F2, a%5E2=13%2F4, b%5E2=13%2F2, a=sqrt%2813%29%2F2, b=sqrt%2813%2F2%29=sqrt%28expr%2813%2F2%29%2Aexpr%282%2F2%29%29=sqrt%2826%29%2F2

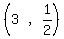The center is (h,k) = %28matrix%281%2C3%2C3%2C%22%2C%22%2C1%2F2%29%29, the big green dot below.

We draw the defining rectangle with (h,k) as its center, its vertical
dimension is 2a = sqrt%2813%29, and its horizontal dimension is 2b = sqrt%2826%29.

We extend the diagonals of the defining rectangle, since they are the
asymptotes of the hyperbola. Then we sketch in the hyperbola:



Edwin