SOLUTION: This is so hard for me to grasp for some reason. Can someone help me, please? Convert the following partial sums into sigma notation and evaluate the sums: a) 1/(1*2^2) + 1/(2*3

Evaluating is just basic fraction math:







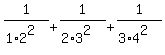
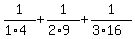
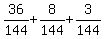
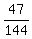For the summation, I'll try some coloring to see if that helps:



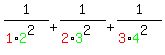Notice that the 1's on top stay the same.
Notice that the 2 exponents on the bottom stay the same in all terms.
Notice that the red numbers go 1,2,3
Notice that the green numbers go 2,3,4, just 1 more than the red numbers.
So if k represents a red number, then the corresponding green number is k+1.

So each term is of the form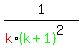 

And k starts at 1 and goes to 3.  We indicate that
with


-------------------

The evaluation is simple addition, getting 45.

This one is easier than the first one.

They are the first 5 multiples of 3.  They are



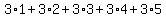The 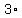 is the same on all the terms,
The numbers after the 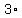 go 1,2,3,4,5
So if k represents the numbers on the right of the ,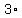
then k starts at 1 and goes up to and including 5:

So each term has the form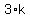 

The summation is



Edwin