Question 967928: http://www.algebra.com/tutors/students/your-answer.mpl?question=967815
I am asking how did u get the discriminant less than zero. Did the question says tell . Please explain.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Not being in your class, I have no idea how you were expected to solve this problem. The ways you can solve a problem vary, depending on what you have learned so far. A fifth grader may have only one way to solve it, but a colleg professor may be able to think of many different ways.
Maybe you were expected to try different integer values for p,
and graph the resulting functions using a graphing calculator.
Maybe the expected approach is the one the other poster(s) tried to explain,
which apparently made no sense to you.
Let's try this a different way. Maybe you'll like it better.
The original question was:
"Find the smallest integer p such that x^2-2x+p is always greater than 3".

We know that a square, like 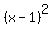 is never negative. is never negative.

For  , ,  and and  . .
Otherwise  is greater than is greater than  . .
 is the minimum value for is the minimum value for  . .
We need 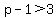 <---> <--->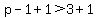 <---> <--->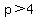 . .
Because the problem asks for the smallest 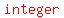 that makes x^2-2x+p always greater than 3, that makes x^2-2x+p always greater than 3,
and the smallest integer  such that such that 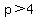 is is  , ,
the answer is  . .
Does your teacher expect you to talk about the discriminant of a quadratic equation and/or the quadratic formula?
Maybe, but I agree with professor Peter Alfeld, that there is no need to memorize such things.
(I do remember them, because they made me memorize such things,
and maybe you will experience the same,
because most people believe that just for expediency,
you should memorize stuff that you could deduce on your own).
|
|
|