SOLUTION: I need to use the Gaussian elimination method on the following: For a circuit, the currents i1, i2, and i3 measured in amperes, are determined by the following linear equations

Algebra ->  Matrices-and-determiminant -> SOLUTION: I need to use the Gaussian elimination method on the following: For a circuit, the currents i1, i2, and i3 measured in amperes, are determined by the following linear equations      Log On


   

Question 967753: I need to use the Gaussian elimination method on the following:

For a circuit, the currents i1, i2, and i3 measured in amperes, are determined by the following linear equations:
-i1 + 4i3 = 3
5i1 - 3i2 = 26
-3i1 +6i2 = -21
Any help would be very helpful.
Thanks in advance
Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!

Let's introduce new variables  x = i1,  y=i2  and  z=i3  for brevity.
Then you need to solve the system of three linear equations in three unknowns

-x   +         4z = 3,
5x   - 3y         = 26,
-3x + 6y         = -21

by the Gauss's elimination method.

Notice that your system just contains the sub-system of two linear equations in two unknowns  x  and  y.  It is the system consisting of the second and the third equations.
Its facilitates the solution.

So,  we need to solve this sub-system,  which is

5x   - 3y = 26,
-3x + 6y = -21.

Multiply the first equation of these two by  2  and add to the second equation to eliminate  y.  You will get

    10x   - 6y = 52,
+
     -3x + 6y = -21.
--------------------
      7x          = 31.

It gives you the solution for  x:  x = 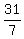31%2F7.

Next, substitute it to any of the second or the third equation of the original system.  It gives you the solution for  y.

Then substitute the found values of  x  and  y  into the first equation,  and you will get the solution for  z.

Good luck.

-------------------------------------------------------------------------
Comment from student: Hi ikleyn, thanks for the response. How would I solve this question using an augmented matrix and using gaus elimination? Thanks again for the help.
-------------------------------------------------------------------------

OK, let's do this.

Your augmented matrix is
%28matrix%283%2C+4%2C+-1%2C+0%2C+4%2C+3%2C+5%2C+-3%2C+0%2C+26%2C+-3%2C+6%2C+0%2C+-21%29%29.

Multiply the first row by  5  and add to the second row to eliminate  x  in the second equation.  You will get
%28matrix%283%2C+4%2C+-1%2C+0%2C+4%2C+3%2C+0%2C+-3%2C+20%2C+145%2C+-3%2C+6%2C+0%2C+-21%29%29.

Next,  multiply the first row by  -3  and add to the third row to eliminate  x  in the third equation.  You will get
.

OK,  we just made the zeroes in the first column below  "-1".

Now,  multiply the second row of the last matrix by  2  and add to the third row to eliminate  y  in the third equation.  You will get
%28matrix%283%2C+4%2C+-1%2C+0%2C+4%2C+3%2C+0%2C+-3%2C+20%2C+145%2C+0%2C+0%2C+28%2C+260%29%29.

Thus you just completed the elimination process:  you transformed your original matrix to the upper triangle matrix.
Hence,  the solution for  z  is  z = 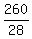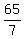260%2F28 = 65%2F7 = 92%2F7.

Now you should make back-substitution.
Substitute the found value of  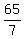z = 65%2F7  into the equation
-3y + 20z = 145   (in accordance with the second row of the last matrix).  It will give you the solution for  y.

Then back-substitute the found values of  y  and  z  into the very first equation and find  x.