SOLUTION: How would a tank that has a volume of approximately 150 litres and a maximum length of 1.30m be? show all calculations, lengths, and angles that any lines make to the horizontal.

Algebra ->  Trigonometry-basics -> SOLUTION: How would a tank that has a volume of approximately 150 litres and a maximum length of 1.30m be? show all calculations, lengths, and angles that any lines make to the horizontal.       Log On


   

Question 967594: How would a tank that has a volume of approximately 150 litres and a maximum length of 1.30m be? show all calculations, lengths, and angles that any lines make to the horizontal.
the tank that i have designed has the same 'shape' on either end, and a uniform cross-section. the angled lines have different lengths
I must show my use of trigonometry of how i came up with my final design and i need help with this.
Thanks
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
From your description, I do not get the exact idea of what your design is.
However, I may be able to guess something similar, and the explanation of my calculations could be useful to you.
A uniform cross-section would mean a cylinder of a right rectangular prism, but those shapes are rather boring, and do not show use of trigonometry.
I suspect your design is a cylinder with pointy ends added, something that from the side looks like this
, end on looks like this ,
and from the top looks like this .
You do not need trigonometry for that, unless you care about the exact angles at the pointy ends.
In my drawing, if we call the diameter of the cylindrical part D=2R (R= radius),
the pointy ends are %282%2F3%29D=%284%2F3%29R up from the bottom (%281%2F3%29D from the top),
and %282%2F3%29D=%284%2F3%29R away from the of end
of the cylindrical part.
That makes for a 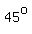45%5Eo upslope,
and a downslope with an angle theta such that
tan%28theta%29=%28%281%2F3%29D%29%2F%28%282%2F3%29D%29=1%2F2 , so theta=about26.6%5Eo .
It also makes that %282%2F3%29D=%284%2F3%29R%29 away from the of cylinder end distance the height of the cone.
Also, in my drawing, the length of the cylindrical part is L=%285%2F3%29D=%2810%2F3%29R .

The cross section of the cylindrical part (and the bases of the cones)
are circles of radius R ,
and each has a surface of pi%2AR%5E2 .
The volume of the cylindrical part would be
V%5Bcyl%5D=pi%2AR%5E2%2AL=pi%2AR%5E2%2A%2810%2F3%29R=pi%2A%2810%2F3%29%2AR%5E3 .
The volume of a cone is 1%2F3 times the surface area of the base, times the height.
(It does not matter if it is a right cone,
with the vertex right above the center of the base)
or an oblique cone, like those in my design,
with the vertex not directly above the center of the base).
So the volume of each conical end is
V%5Bcone%5D=%281%2F3%29%2Api%2AR%5E2%2A%284%2F3%29%2AR=%284%2F9%29%2Api%2AR%2A3 .
The total volume of my tank is


Considering that 1 liter is 1 cubic decimeter, or 1000 cubic centimeters, for exactly 150 L, I need
pi%2838%2F9%29%2AR%5E3=150000cm%5E3--->R%5E3=150000%2A9%2F%2838pi%29cm%5E3--->R%5E2=11308.37754cm%5E3-->R=about22.44cm

If I use R=22.44cm , my cylinder will have that radius,
The length will be L=%2810%2F3%29R=%2810%2F3%29%2A22.44cm=74.82cm=0.7482m ,
and the height of each cone end section will be
%284%2F3%29R=%284%2F3%2922.44cm=29.92cm .