Question 967533: whats x and y for 8x+7y=-11 and 4x-3y=14?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You need to solve the system of two linear equations in 2 unknowns

Multiply the second equation by 2 and then distract from the first equation. You will get
8x + 7y = -11,
-
8x - 6y = 28
-------------
13y = 28 + 11 = 39.
Hence, y = 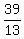 = 3. = 3.
Now, substitute the found value of y = 3 into the either equation of your original system, for example, into the first equation. You will get
8x +7*3 = -11, or
8x + 21 = -11, or
8x = -11 - 21 = -32.
Hence, x = 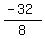 = -4. = -4.
Answer. The solution of the system is x = -4, y = 3.
We applied here the Elimination method.
For solving systems of two linear equations in three unknowns see the lessons
- Solution of the linear system of two equations in two unknowns by the Substitution method,
- Solution of the linear system of two equations in two unknowns by the Elimination method,
- Solution of the linear system of two equations in two unknowns using determinant,
- Geometry interpretation of the linear system of two equations in two unknowns and
- Solving word problems using linear systems of two equations in two unknowns.
|
|
|