SOLUTION: Find the area of quadrilateral ABCD whose sides are 9m 40m 28m 15m and angle ABC=90°

Algebra ->  Triangles -> SOLUTION: Find the area of quadrilateral ABCD whose sides are 9m 40m 28m 15m and angle ABC=90°      Log On


   

Question 965826: Find the area of quadrilateral ABCD whose sides are 9m 40m 28m 15m and angle ABC=90°
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Find the area of quadrilateral ABCD whose sides are 9m 40m 28m 15m and angle ABC=90°
-------------
Assuming AB = 9 and BC = 40:
Put A at the Origin, B at (0,9), C at (40,9)
Point D is the intersection of 2 circles, one centered at A with r = 15 and one centered at C with r = 28.
--> x^2 + y^2 = 225 and
(x-40)^2 + (y-9)^2 = 784
Find the intersection of the 2 circles:
x^2 + y^2 = 225
x^2 + y^2 - 80x - 18y = -897
------------------------------------- subtract
80x + 18y = 1122 is the equation of the line passing thru the 2 intersections of the circles.
--> y = (561 - 40x)/9
x^2 + y^2 = 225
Sub for y
x^2 + ((561 - 40x)/9)^2 = 225
81x^2 + (561 - 40x)^2 = 225*81 = 18225
81x^2 + 1600x^2 - 44880x + 314721 = 18225
1681x^2 - 44880x + 296496 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1681x%5E2%2B-44880x%2B296496+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-44880%29%5E2-4%2A1681%2A296496=20575296.

Discriminant d=20575296 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--44880%2B-sqrt%28+20575296+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-44880%29%2Bsqrt%28+20575296+%29%29%2F2%5C1681+=+14.6983938132064
x%5B2%5D+=+%28-%28-44880%29-sqrt%28+20575296+%29%29%2F2%5C1681+=+12

Quadratic expression 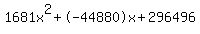1681x%5E2%2B-44880x%2B296496 can be factored:
1681x%5E2%2B-44880x%2B296496+=+%28x-14.6983938132064%29%2A%28x-12%29
Again, the answer is: 14.6983938132064, 12. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1681%2Ax%5E2%2B-44880%2Ax%2B296496+%29

==============
x = 14.6984
--> y = -2.9929
D is (14.6984,-2.9929)
======================
Write the points in order. I'll use (14.7,-3) for D
A...B...C...D....A
0...0..40..14.7..0
0...9...9..-3....0
Add the diagonal products starting at the upper left.
0+0-120+0 = 120
Add the diagonal products starting at the lower left.
0+360+132.3+0 = 492.3
------------
Find the difference = 492.3 - 120 = 372.3
The area is 1/2 that
Area = 186.15 sq units