Question 965404: Write an equation in slope-intercept form of a linear function f whose graph satisfies the given conditions.
The graph of f passes through (-6, 4) and is perpendicular to the line that has an x-intercept of 2 and a y–intercept of -4.
Found 2 solutions by josgarithmetic, MathLover1:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! perpendicular to the line that has an x-intercept of 2 and a y–intercept of -4.
Negative reciprocal of (1/2) is that described slope.
Meaning,  . .
Continuing with point slope form,

Do what you need to do.....
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
slope-intercept form:  where where  is a slope and is a slope and  is y-intercept is y-intercept
given:
the graph of f passes through ( , , ) )
and
is perpendicular to the line that has an x-intercept of  and a y–intercept of and a y–intercept of 
 if ( if ( , , ) on a line, then we have ) on a line, then we have
 ........eq.1 ........eq.1
if line is perpendicular to the line that has an x-intercept of  and a y–intercept of and a y–intercept of  , then our line has a slope negative reciprocal to the slope of the line that has an x-intercept of , then our line has a slope negative reciprocal to the slope of the line that has an x-intercept of  and a y–intercept of and a y–intercept of 
first find the equation of the line that has an x-intercept of  and a y–intercept of and a y–intercept of 
if the line that has an x-intercept of  , then the point ( , then the point ( , , ) is on a line ) is on a line
so, we have

 ........... eq.2 ........... eq.2
if the line that has an y-intercept of  , then the point ( , then the point ( , , ) is on a line ) is on a line
so, we have


 .......substitute in eq.2 and find .......substitute in eq.2 and find 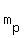
 ........... eq.2 ........... eq.2


so, the equation of the line is perpendicular to the line that has an x-intercept of  and a y–intercept of and a y–intercept of  is is

since the slope is  , our line will have the slope , our line will have the slope  which is is the negative reciprocal of the which is is the negative reciprocal of the 
so far we have  and we need to find and we need to find 

use  ........eq.1, substitute ........eq.1, substitute 





so, the equation of a line we are looking for is: 

|
|
|