SOLUTION: An airplane takes 3.6 hours to fly 1800 miles against the wind. It only takes the plane 3 hours to return 1800 miles with the wind. Assuming that the plane flies at a constant spee

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: An airplane takes 3.6 hours to fly 1800 miles against the wind. It only takes the plane 3 hours to return 1800 miles with the wind. Assuming that the plane flies at a constant spee      Log On


   

Question 965150: An airplane takes 3.6 hours to fly 1800 miles against the wind. It only takes the plane 3 hours to return 1800 miles with the wind. Assuming that the plane flies at a constant speed, how long will it take it to fly 3300 miles when there is no wind?
Found 3 solutions by amarjeeth123, josgarithmetic, MathTherapy:
Answer by amarjeeth123(569) About Me  (Show Source):
You can put this solution on YOUR website!
Let the speed of the airplane be x mph
Let the speed of the wind be y mph
Speed=Distance/Time
When it is flying against the wind,
x-y=1800/3.6=500.........equation 1
When it flies with the wind,
x+y=1800/3=600..........equation 2
Adding equations 1 and 2 we get,
x+y+x-y=500+600
2x=1100
x=550 mph
y=50 mph
The speed of the plane is 550 mph.
Time taken to fly 3300 miles without the wind=Distance/Speed=3300/550=6 hours
Answer=6 hours

Answer by josgarithmetic(39615) About Me  (Show Source):
You can put this solution on YOUR website!
_______________________rate_______________time____________distance
AGAINST________________r-w_________________q_______________d
WITHWND________________r+w_________________p_______________d

KNOWN:
q=3.6
p=3.0
d=1800
UNKNOWN:
r, speed without wind
w, speed of the wind
The focus of the solution is for finding r.

system%28%28r-w%29q=d%2C%28r%2Bw%29p=d%29

system%28qr-qw=d%2Cpr%2Bpw=d%29

-qw=d-qr

w=d%2F%28-q%29-qr%2F%28-q%29

w=-d%2Fq%2Bqr%2Fq

highlight_green%28w=qr%2Fq-d%2Fq%29




Substitute for w in the other equation:

pr=d-pw

r=d%2Fp-pw%2Fp

r=d%2Fp-%28qr%2Fq-d%2Fq%29%2Fp

r=d%2Fp-%28qr%2F%28pq%29-d%2F%28pq%29%29

r=d%2Fp%2Bd%2F%28pq%29-qr%2F%28pq%29

r%2B%28q%2F%28pq%29%29r=d%2Fp%2Bd%2F%28pq%29

r%281%2Bq%2F%28pq%29%29=%28d%2Fp%29%28q%2Fq%29%2Bd%2F%28pq%29

r%281%2B1%2Fp%29=%28dq%2Bd%29%2F%28pq%29

r%28p%2Fp%2B1%2Fp%29=%28dq%2Bd%29%2F%28pq%29

r%28p%2B1%29%2Fp=%28dq%2Bd%29%2F%28pq%29

r=%28p%2F%28p%2B1%29%29%28%28dq%2Bd%29%2F%28pq%29%29

r=%28dq%2Bd%29%2F%28%28p%2B1%29%28pq%29%29
maybe further steps, fully multiply denominator,

highlight%28r=%28dq%2Bd%29%2F%28p%5E2%2Aq%2Bpq%29%29

That is the formula for the rate of the airplane without the wind.
Now just substitute the values assigned and find the value for r.

This could have been easier if not done completely in symbols, but maybe you will have
other uniform travel rate exercises which are of the same form.

Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!

An airplane takes 3.6 hours to fly 1800 miles against the wind. It only takes the plane 3 hours to return 1800 miles with the wind. Assuming that the plane flies at a constant speed, how long will it take it to fly 3300 miles when there is no wind?
Let speed in calm air be S, and wind, W

To travel 1,800 miles in 3.6 hours against the wind, total speed = 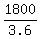1800%2F3.6, or 500 mph

We then have: S - W = 500 ------- eq (i)



To travel 1,800 miles in 3 hours with the wind, total speed = 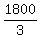1800%2F3, or 600 mph

We then have: S + W = 600 ------- eq (ii)

2S = 1,100 ------- Adding eqs (ii) & (i)

S, or speed in still air = 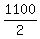1100%2F2, or 550 mph



Time taken to travel 3,300 miles in calm air = 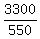3300%2F550, or highlight_green%286%29 hours