SOLUTION: i don't have the actual graph but it says the graph below shows the solution to y=2x-5. then the next question says (part a): graph the solution to y= -1/2x on the same coordinate

Algebra ->  Linear-equations -> SOLUTION: i don't have the actual graph but it says the graph below shows the solution to y=2x-5. then the next question says (part a): graph the solution to y= -1/2x on the same coordinate       Log On


   

Question 964276: i don't have the actual graph but it says the graph below shows the solution to y=2x-5. then the next question says (part a): graph the solution to y= -1/2x on the same coordinate plan. (part b) says: using the graph you drew in (part a), what point is the solution to the system of equations y=-1/2x and y=2x-5? (part c)says:suppose you graph the solutions to y=2x-5 and y=5/2x+5 on the same coordinate plane and notice that the lines do not intersect. is there a solution to the system of equations? Explain your reasoning's pleasee
okay the next questions is
Amanda found the equation 10x+5y=20 in the "linear equations" chapter of her math book. (part a) says: what is an equation that can be written with Amanda's equation to form a pair of linear equations such that the system of equations has exactly one solution.
Part b says: what is an equation that can be written with Amanda's equation to form a pair of linear equations such that the system of equations has infinitely many solutions?
Part C: what is an equation that can be written with Amanda's equation to form a pair of linear equations such that there is no solution?
Part d: how many possible answers are there to Parts a,b,and c? explain your reasoning please
Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
the graph below shows the solution to y=2x-5.
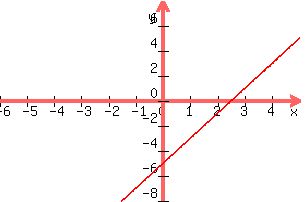
+graph%28+300%2C+200%2C+-6%2C+5%2C+-8%2C+8%2C+2x-5%29+
:
then the next question says (part a): graph the solution to y= -1/2x on the same coordinate plan.
+graph%28+300%2C+200%2C+-6%2C+5%2C+-8%2C+8%2C+2x-5%2C+-.5x%29+
:
(part b) says: using the graph you drew in (part a), what point is the solution to the system of equations y=-1/2x and y=2x-5?
You can see the graphs intersect where x=2, y=-1
:
(part c)says:suppose you graph the solutions to y=2x-5 and y=5/2x+5 on the same coordinate plane and notice that the lines do not intersect. is there a solution to the system of equations?
+graph%28+300%2C+200%2C+-6%2C+5%2C+-8%2C+8%2C+2x-5%2C+2.5x%2B5%29+
Explain your reasoning: they do not intersect on this graph but you can see they are not parallel, so the do intersect somewhere, a large scale grph shows this
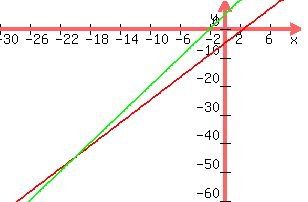
+graph%28+300%2C+200%2C+-30%2C+10%2C+-60%2C+10%2C+2x-5%2C+2.5x%2B5%29+
You can see they intersect at -20, -45, so that is the solution for those equations
:
okay the next questions is
Amanda found the equation 10x+5y=20 in the "linear equations" chapter of her math book.Convert the equation to the slope/intercept form
10x + 5y = 20
simplify, divide by 5
2x + y = 4
y = -2x + 4
:
(part a) says: what is an equation that can be written with Amanda's equation to form a pair of linear equations such that the system of equations has exactly one solution.
Choose an equation that has a positive slope to ensure they will intersect
y = x - 5
looks like this
+graph%28+300%2C+200%2C+-6%2C+5%2C+-8%2C+8%2C+-2x%2B4%2C+x-5%29+
You can see that this pair of equations has a single solution 3, -2
:
Part b says: what is an equation that can be written with Amanda's equation to form a pair of linear equations such that the system of equations has infinitely many solutions? This happens when the 2nd equation is the same as the first.
:
Part C: what is an equation that can be written with Amanda's equation to form a pair of linear equations such that there is no solution?
Equations with the same slope are parallel, so no solution
y = -2x + 4 and y = -2x + 2
+graph%28+300%2C+200%2C+-6%2C+5%2C+-8%2C+8%2C+-2x%2B4%2C+-2x%2B2%29+
Part d: how many possible answers are there to Parts a,b,and c? explain your reasoning please