Question 964132: use the rational zeros theorem to find all zeros of the polynomial. Use the zeros to factor f over the real numbers.
f(x)=x^3-5x^3-61x-55 show work
Answer by josgarithmetic(39621)   (Show Source):
You can put this solution on YOUR website! Possible roots to check for would be -55, -11, -5, -1, 1, 5, 11, 55.
There would be no more than eight synthetic divisions to perform in order to check for roots. With so many to check, software to help would be preferable. Otherwise, on paper, start with -5, -1, 1, and 5. Simpler less advanced factoring might be enough after that.
First tried -5, myself.
__________-5____|______1_______-5_______-61_______-55
________________|
________________|______________-5________50________55
________________|________________________________________
_______________________1_________-10_______-11_______0
One root or zero is  , and the quadratic resulting is 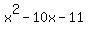 , easily factorable into  .
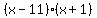The zeros are -5, 11, -1.
|
|
|
