Question 963469: Part I.
G(x) = -x4 + 32x2 +144
a. Show whether G is an even, odd function or neither. If itís even/odd, identify the property of its graph. (Must show your work)
(Help: To show that G is an even function, you must show that G(-x) = G(x), and G is an odd function you must show that G(-x) = -G(x), for ex. F(x) = x3 Ė 3x is an odd function, since:
F(-x) = (-x)3-3(-x) = -x3+3x = -(x3-3x) = -F(x), thus F is an odd function. And by definition odd function has graph symmetric about the origin).
b. There is a local maximum value of 400 at x = 4, determine the second local maximum value (Use property of the graph of an even/odd function from part a:
(Hints: if (x, f(x)) is a point on the graph of an even function f, then (-x, f(-x)) is symmetric about the y-axis since f(-x)= f(x) is also on the graph of f).
c. Suppose the area under the graph of G between x = 0, and x = 6, that is bounded below by the x-axis is 1612.8 square units, Using the result from part a to determine the area under the graph of G between x = -6 and x = 0, bounded below by the x-axis.
(Hints: Use property of the graph of an even/odd function).
Part II.
a. Choose a library function, then use the library function, and describe how to graph the function:
Y = (x Ė 3)2 Ė 5 (just describe without graphing).
(Hints: Y = |x + 4| + 7, then library function is f(x) = |x| absolute value function, then the graph of Y can be obtained from the graph of f by shifting the graph of f to the left 4 units, and up 7 units).
b. Use the library function f(x) =√x Write the function y obtained from f(x) =√x by shifting the graph of f 4 units to the left, and down 2 unit.
(Hints: f(x) = x2; f(x) = x3; f(x) = √x; f(x) = |x|, etc.. each is a library function. If y= f(x-h), then graph of y can be obtained from graph of f by shifting the graph of f to the right h units, etcÖPlease review transformations of graphs = shifting technique to answer both questions of part a, and b).
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! Part I.
a.
A function is "even" when:
 for all for all 
A function is "odd" when:
 for all for all 
check your function: is it "even"
f(x) = f(-x) for all x
 ...since ...since 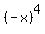 will be same as will be same as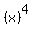 , and , and 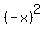 will be same as will be same as 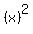 , we have , we have

so, your function is 
is it odd:
 for all for all 

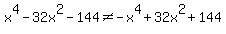 .......your function is not .......your function is not 
b.
There is a local maximum value of  at at  , determine the second local maximum value: , determine the second local maximum value:
( , , ) =( ) =( , ,  ) )
find




so, if ( , ,  ) is a point on the graph of an even function G, then ( ) is a point on the graph of an even function G, then ( , ,  ) is symmetric about the y-axis since ) is symmetric about the y-axis since  is also on the graph of G is also on the graph of G
c. Suppose the area under the graph of G between  , and , and  , that is bounded below by the x-axis is , that is bounded below by the x-axis is 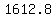 square units, Using the result from part a to determine the area under the graph of G between square units, Using the result from part a to determine the area under the graph of G between  and and  , bounded below by the x-axis. , bounded below by the x-axis.
Graphs of even and odd functions have following properties:
If function is even then its graph is symmetric about y-axis.
If function is odd then its graph is symmetric about origin.
so, because the graph is symmetric about y-axis, the area under the graph of G between  and and  is bounded below by the x-axis is is bounded below by the x-axis is 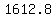 square units square units
Part II.
a.
Choose a library function, then use the library function, and describe how to graph the function:
 (just describe without graphing). (just describe without graphing).
library function is 
and  can be obtained from the graph of can be obtained from the graph of  by shifting the graph of f to the right by shifting the graph of f to the right  units, and down units, and down  units units
b.
Use the library function  Write the function y obtained from Write the function y obtained from  by shifting the graph of f by shifting the graph of f  units to the left, and down units to the left, and down  unit. unit.


|
|
|