Question 961723: A vending machine has $6.30 in it. There are 52 coins total and the machine only accepts nickels, dimes, and quarters. There are five more dimes than nickels. How many of each coin are in the machine.
Found 3 solutions by CubeyThePenguin, josgarithmetic, ikleyn:
Answer by CubeyThePenguin(3113)   (Show Source):
You can put this solution on YOUR website! n = number of nickels
d = number of dimes
q = number of quarters
n + d + q = 52
d = n + 5
5n + 10d + 25q = 630
(substituting d = n + 5 into the first and third equations)
2n + q = 47
15n + 25q = 580
Multiply the first equation by 25 (eliminating q)
50n + 25q = 1175
-15n - 25q = -580
---------------------
35n = 595
n = 17
d = 17 + 5 = 22
q = 52 - 17 - 22 = 13
---> There are 17 nickels, 22 dimes, and 13 quarters.
Answer by josgarithmetic(39617)  (Show Source):
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
A vending machine has $6.30 in it. There are 52 coins total and the machine only accepts nickels,
dimes, and quarters. There are five more dimes than nickels. How many of each coin are in the machine ?
~~~~~~~~~~~~~
It is a typical problem to be solved using only one single unknown and only one single equation.
Let x be the number of nickels.
Then the number of dimes is (x+5), according to the condition.
The quarters are the rest coins, and their number is (52-x-(x+5)) = (47-2x).
Having it, you write the total money equation
5x + 10(x+5) + 25*(47-2x) = 630 cents.
Simplify and solve
5x + 10x + 50 + 25*47 - 50x = 630
-35x = 630 - 50 - 25*47 = -595
x = 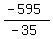 = 17.
ANSWER. 17 nickels, 22 dimes and the rest 52 - 17-22 = 13 coins are quaters.
CHECK. 17*5 + 22*10 + 13*25 = 630 cents, in total. ! Correct !
Solved.
--------------------
It is how this problem is intended and is expected to be solved.
Only the persons UNFAMILIAR with a standard basic mathematical education principles,
like @josgarithmetic or @Penguin, may think differently . . .
|
|
|
