Question 961639: Bob owns many identical apartment units. When rent is 1000 dollars per month per
unit all 100 of his apartment units are rented. Bob estimates that for each 50 dollar increase in
rent 2 apartment units will go unrented. Find how much money Bob should charge to rent one
unit for one month so that he maximizes his total revenue.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! these can be tricky.
it's a matter of setting it up properly.
revenue is equal to the rent per unit times the number of units.
you start with revenue = 1000 * 100
now every time the rent goes up 50 dollars, the number of units goes down by 2.
if you let x represent the number of times the rent goes up 50 dollars, then the rent portion of the equation becomes 1000 + 50x.
when the rent goes up 50 dollars, the number of units rented goes down by 2.
the number of units then becomes 100 - 2x.
your revenue equation becomes:
revenue = (1000 + 50x) * (100 - 2x)
when x is 0, the revenue is 1000 * 100
when x is 1, the revenue is 1000 + 50 and the number of units is 100 - 2.
when x is 2, the revenue is 1000 + 100 and the number of units is 100 - 4.
i believe that meets the requirements of the problem.
let y = revenue
equation becomes y = (1000 + 50x) * (100 - 2x)
you want to put this equation into standard form of ax^2 + bx + c = 0
simplify the equation to get:
y = 100,000 - 2000x + 5000x - 100x^2
combine like terms to get:
y = 100,000 + 3,000x - 100x^2
reorder the terms of equation in descending order of degrees to get:
y = -100x^2 + 3,000x + 100,000
the max/min point is at x = -b/2a.
in this equation:
a = coefficient of x^2 term equals -100
b = coefficient of x term equals 3,000
c = constant term equals 100,000
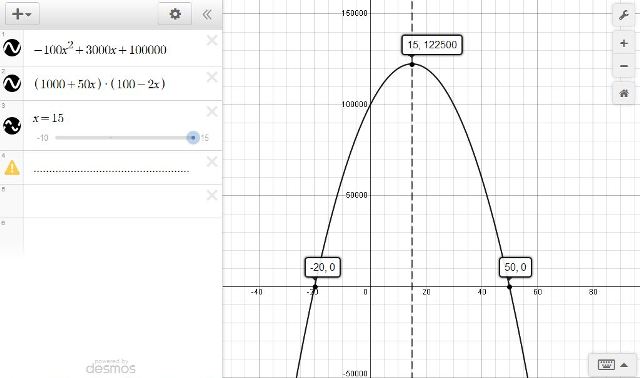
x = -b/2a becomes x = -3,000 / -200 which becomes 15.
the equation will be at a maximum point when x = 15.
when x = 15, the value of y is equal to -100(15)^2 + 3,000(15)+100,000 which is equal to -22,500 + 45,000 + 100,000 which is equal to 122,500.
your maximum revenue is when x is equal to 15.
when that occurs, your maximum revenue is equal to 122,500.
the graph of your equation is shown below:
|
|
|