SOLUTION: Let t be a real number with cos(t)=3/7, 3pi/2 < t < 2pi Find the exact value for each of the following: a. sin(t+3pi/2) b. sec(-t) c. cos(2pi) d.cos(4pi/3 - t) Pl

Algebra ->  Trigonometry-basics -> SOLUTION: Let t be a real number with cos(t)=3/7, 3pi/2 < t < 2pi Find the exact value for each of the following: a. sin(t+3pi/2) b. sec(-t) c. cos(2pi) d.cos(4pi/3 - t) Pl      Log On


   

Question 960796: Let t be a real number with cos(t)=3/7, 3pi/2 < t < 2pi Find the exact value for each of the following:
a. sin(t+3pi/2)
b. sec(-t)
c. cos(2pi)
d.cos(4pi/3 - t)

Please explain what these means how these are solved I have to understand!
Thank you! in advance
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
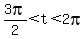Let t be a real number with cos%28t%29=3%2F7, 3pi%2F2+%3C+t+%3C+2pi Find the exact value for each of the following: 
therefore angle t is in the 4th quadrant.

a. sin(t+3pi/2) 
Use the identity sin%28A%2BB%29=sin%28A%29cos%28B%29%2Bcos%28A%29sin%28B%29

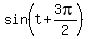
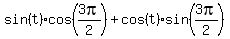
sin%28t%2B3pi%2F2%29%22%22=%22%22sin%28t%29cos%283pi%2F2%29%2Bcos%28t%29sin%283pi%2F2%29
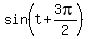
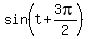
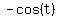
sin%28t%2B3pi%2F2%29%22%22=%22%22sin%28t%29%280%29%2Bcos%28t%29%28-1%29
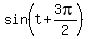
sin%28t%2B3pi%2F2%29%22%22=%22%22-cos%28t%29
sin%28t%2B3pi%2F2%29%22%22=%22%22-3%2F7

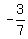
b. sec(-t)
Multiplying an angle by -1 moves the angle t from 4th quadrant to 1st quadrant,
and the secant is the reciprocal of the cosine and is positive in 1st and 4th
quadrants. So

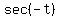
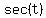
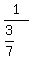
sec%28-t%29%22%22=%22%22sec%28t%29%22%22=%22%221%2Fcos%28t%29%22%22=%22%221%2F%283%2F7%29%22%22=%22%227%2F3

c. cos(2pi)
That's just 1.  It has nothing to do with t.

d.cos(4pi/3 - t) 
Use the identity cos%28A-B%29=cos%28A%29cos%28B%29%2Bsin%28A%29sin%28B%29

cos%284pi%2F3-t%29=cos%284pi%2F3%29cos%28t%29%2Bsin%284pi%2F3%29sin%28t%29
cos%284pi%2F3-t%29=%28-1%2F2%29%283%2F7%29%2B%28-sqrt%283%29%2F2%29sin%28t%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28-sqrt%283%29%2F2%29sin%28t%29

Use identity sin%28A%29=+%22%22+%2B-+sqrt%281-cos%5E2%28A%29%29
since t is in quadrant 4 where sine is negative we use 
the negative:

cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28-sqrt%283%29%2F2%29%28-sqrt%281-cos%5E2%28t%29%29%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28sqrt%283%29%2F2%29%28sqrt%281-cos%5E2%28t%29%29%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28sqrt%283%29%2F2%29%28sqrt%281-%283%2F7%29%5E2%29%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28sqrt%283%29%2F2%29%28sqrt%281-9%2F49%29%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28sqrt%283%29%2F2%29%28sqrt%2849%2F49-9%2F49%29%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28sqrt%283%29%2F2%29%28sqrt%2840%2F49%29%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28sqrt%283%29%2F2%29%28sqrt%2840%29%2F7%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28sqrt%283%29%2F2%29%28sqrt%284%2A10%29%2F7%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%28sqrt%283%29%2F2%29%282sqrt%2810%29%2F7%29
cos%284pi%2F3-t%29=%28-3%2F14%29%2B%282sqrt%2830%29%2F14%29
cos%284pi%2F3-t%29=%28-3%2B2sqrt%2830%29%29%2F14
  


Edwin