|
Question 960775: If f:[0,1]-[0,1] is defined by F(x)=√1-x×x,is it a onto function?If yes,then how to prove it?
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The way F(x) is given with no parentheses to show
what is under the square root and what is not, I can
only guess what the funtion is. I will guess that it
is this:
  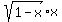
 From the graph it appears as though it is not 'onto'
because the graph does not go above the green line
which I drew only to show that it the graph does not
go into the upper half of the unit square.
To prove that it is not 'onto', we only have to
find a value of y in the interval [0,1] for which
there is no value x such that F(x)=y.
The easiest value of y in closed interval [0,1]
to show that there is no value of x in [0,1]
such that F(x)=y, is y=1
On the open interval (0,1) both factors of F(x),
From the graph it appears as though it is not 'onto'
because the graph does not go above the green line
which I drew only to show that it the graph does not
go into the upper half of the unit square.
To prove that it is not 'onto', we only have to
find a value of y in the interval [0,1] for which
there is no value x such that F(x)=y.
The easiest value of y in closed interval [0,1]
to show that there is no value of x in [0,1]
such that F(x)=y, is y=1
On the open interval (0,1) both factors of F(x), 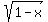 and and  are positive and strictly less than 1. And at the endpoints x=0,
and x=1, F(x) = 0.
Therefore F(x) is never equal to 1 on the interval [0,1]
Therefore F(x) is not 'onto'.
Edwin
are positive and strictly less than 1. And at the endpoints x=0,
and x=1, F(x) = 0.
Therefore F(x) is never equal to 1 on the interval [0,1]
Therefore F(x) is not 'onto'.
Edwin
|
|
|
| |