Question 960677: It takes 4.5 hours for a ship moving downriver to get from port A to port B. The return journey takes 6.3 hours. The river flows at 40 meters per minute. What is the distance between the two ports?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! It takes v hours for a ship moving downriver to get from port A to port B. The return journey takes u hours. The river flows at c meters per minute. What is the distance d between the two ports?
________________rate____________time___________distance(in meters)
downriv_________r+c______________v_____________d
upriver_________r-c______________u_____________d
The rate unit is METERS per MINUTE, but this is not convenient with times being in hours. Suggestion is change the river flow rate unit into KILOMETERS per HOUR. This way, the data table will show columns for rate KILOM per HOUR, time HOURS, distance KILOMETERS.
UNIT CONVERSION
c = river flow rate, 
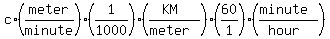
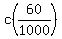
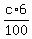
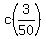
-
The NEATER way to continue this is to assign  , ,
and you can continue to expect r is in unit of kilometers per hour.
With that, you can continue with the data table nearly unchanged:
________________rate____________time___________distance(in KILOmeters)
downriv_________r+c______________v_____________d
upriver_________r-c______________u_____________d
Now, c=(3/50)40, v=4.5, u=6.3.
r=unknown rate for the ship if traveling in still water.
d=unknown distance between A and B.
Form this system of linear equations in the two UNKNOWN variables r and d.

Note that c simplified to  . .
Solve the system purely in symbolic form first, and especially focus on the final result for the question, d. ______________Substitute the values into the symbolic form result.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It takes 4.5 hours for a ship moving downriver to get from port A to port B. The return journey takes 6.3 hours. The river flows at 40 meters per minute. What is the distance between the two ports?
Distance between ports: 
|
|
|