Draw angle B in 3rd quadrant:
Since sine =  , we make y=-1 and r=5, so that the sin(B)
will be
, we make y=-1 and r=5, so that the sin(B)
will be 

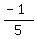 .
.
 But we want cos(B) which is
But we want cos(B) which is  Then we find x by the Pythagorean relation:
Then we find x by the Pythagorean relation:






 Since x goes to the left, we know to take the negative
value
Since x goes to the left, we know to take the negative
value 
 So
So 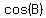



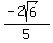

 Now use the formula
Now use the formula
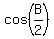

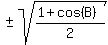 We need to determine whether to use the + or the - sign.
Since B is in the 3rd quadrant,
We need to determine whether to use the + or the - sign.
Since B is in the 3rd quadrant, 
 Therefore
Therefore  is in quadrant 2, and the cosine will be
negative, so
is in quadrant 2, and the cosine will be
negative, so
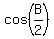

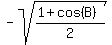
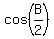

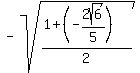 Multiply numerator and denominator by 5 to simplify compound fraction:
Multiply numerator and denominator by 5 to simplify compound fraction:
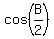

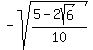 That is the correct answer, but it has a square root within a square
root, and often such an expression can be simplified to the sum or
difference of two square roots of rational numbers. Assume rational
a and b exist so that
That is the correct answer, but it has a square root within a square
root, and often such an expression can be simplified to the sum or
difference of two square roots of rational numbers. Assume rational
a and b exist so that
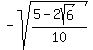

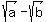 I will assume a difference since a difference occurs under the square
root.
Square both sides
I will assume a difference since a difference occurs under the square
root.
Square both sides
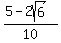

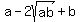 Multiply both sides by 10
Multiply both sides by 10
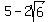

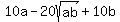 We set rational parts equal and irrational parts equal
We set rational parts equal and irrational parts equal
 ,
, 
 ,
, 

 Solve
Solve  for b,
for b,  Substitute in
Substitute in


 Multiply through by 25a
Multiply through by 25a



 ,
,  Using
Using  , substitute in
, substitute in

 Using
Using  , substitute in
, substitute in

 So we either have
So we either have  ,
, or
or  ,
, But since
But since 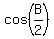 is negative we must choose
the second answer:
is negative we must choose
the second answer:
 ,
, So
So
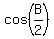

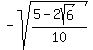

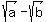

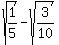

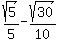 Edwin
Edwin