|
Question 959788: The sum of the digits of a four digit number is 27. The difference of the first two digits is three more than the difference of the last two digits. If the digits are reversed, the original number is 459 more than the new number. Find the original four digit number.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Looks like you have 4 unknowns and only 3 equations; we will have to use some imagination here
:
Let the digits be a, b, c, d
then
1000a + 100b + 10c + d = "the number"
:
Write an equation for each statement
:
The sum of the digits of a four digit number is 27.
a + b + c + d = 27
:
The difference of the first two digits is three more than the difference of the last two digits.
a - b = c - d + 3
Rearrange to
a - b - c + d = 3
:
If the digits are reversed, the original number is 459 more than the new number.
1000a + 100b + 10c + d - 459 = 1000d + 100c + 10b + a
Combine like terms on the left
1000a - a + 100b - 10b + 10c - 100c + d - 1000d = 459
999a + 90b - 90c - 999d = 459
simplify, divide by 9
111a + 10b - 10c - 111d = 51
:
Use elimination on the 1st two equations
a + b + c + d = 27
a - b - c + d = 3
--------------------adding eliminates b and c
2a + 2d = 30
simplify, divide by 2
a + d = 15
:
If a + d = 15, then b + c = 12, (the total is 27)
then
a = (15-d)
and
b = (12-c)
Back to this equation
111a + 10b - 10c - 111d = 51
replace a and b
111(15-d) + 10(12-c) - 10c - 11d = 51
1665 - 111d + 120 - 10c - 10c - 111d = 51
combine like terms
-111d - 111d - 10c - 10c = 51 - 1665 - 120
-222d - 20c = -1734
same as
222d + 20c = 1734
Construct a slope/intercept equation and enter into your graphing calc
c = 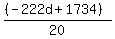 as y= as y=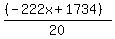
Check the table, d=x, c=y; only one positive integer solution comes up
d = 7
c = 9
fInd a and b
a = 15 - 7
a = 8
and
b = 12-9
b = 3
Find the original four digit number. 8397
:
:
See if that checks out using the reverse number difference
8397
7938
-----
459
:
|
|
|
| |