|
Question 959744: for g(x)=3x^2-12x+6
a,find the values of the x intercepts
b,state the coordinates of the y intercept
c,state the vertex
d,state the axis of symmetry
e,state the direction of the parabola
f,decide whether there is a relative maximum or minimum, then state it
g,graph the function accurately using the above information
h, state the domain
i,state the range
j,state the interval of x where the graph is increasing
k,state the interval of x where the graph is decreasing
Found 2 solutions by josgarithmetic, MathLover1:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! for 
a.find the values of the  intercepts intercepts

 ...since ...since 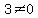 ,then we need to find for what ,then we need to find for what  is is
 ..........use quadratic formula ..........use quadratic formula






solutions
 -exact solution or -exact solution or  approximately approximately
or
 or or  approximately approximately
b.state the coordinates of the  intercept intercept
set  to find the to find the  intercept intercept


the  intercept is at ( intercept is at ( , , ) )
c.state the vertex
the equation for a parabola can also be written in "vertex form":

In this equation, the vertex of the parabola is the point ( , , ). ).
 ...complete square ...complete square



 => =>  and and 
so, ( , , )=( )=( , ,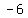 ) )
d.state the axis of symmetry
The line that passes through the vertex and divides the parabola into two symmetric parts is called the axis of symmetry.
here, that is 
e.state the direction of the parabola
since  and if and if 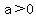 , the parabola opens , the parabola opens 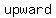
f.decide whether there is a relative maximum or minimum, then state it
the parabola opens  have an minimum have an minimum
g.graph the function accurately using the above information

h. state the domain
 (all real numbers) (all real numbers)
i.state the range
{  element element  : :  } }
j.state the interval of  where the graph is increasing where the graph is increasing
( , , ) )
k.state the interval of  where the graph is decreasing where the graph is decreasing
( , , ) )
|
|
|
| |