Question 959131: Complete the square to determine whether the equation represents an ellipse, a parabola, a hyperbola, a degenerate conic, or results in no solution.
x2 − y2 = 8(x − y) + 1
If the graph is an ellipse, find the center, foci, vertices, and lengths of the major and minor axes. If it is a parabola, find the focus, vertex, and directrix. If it is a hyperbola, find the center, foci, vertices, and asymptotes. (Enter your answers for asymptotes as a comma-separated list of equations. If an answer does not exist, enter DNE.)
Sketch the graph of the equation.
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website! 
 ....since  we see that  and  => => =>
so, it is hyperbola 
and we see that
semimajor axis length  ,
semiminor axis length ,
=> then  => => or 
since  , , the center is at ( ,)
foci:
( , ) | ( ,  )
(( , ) | ( , ))
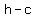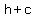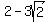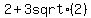approximately:
( , ) | ( ,)
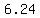vertices:
since the center is at ( , ) = (, ) and the vertices are  units to either side, then vertices are at
( , ) | ( , )
( , ) | ( , )
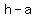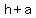asymptotes:
 and 
Sketch the graph of the equation.
|
|
|
