SOLUTION: A college professor has purchased a new bicycle for commuting to class. This bicycle had a purchase price of $600 and depreciates at a constant rate of $55 a year. What is the bi

1. When 0 years have passed, the bicycle is worth $600
2. When 1 year has passed, the bicycle is worth $600-$55 = $545

Let x = the number of years that have passed.
Let y = the worth of the bicycle.

Then, the interpretation of the above two sentences are:

1. When x=0, y=600
2. When x=1, y=545

The mathematical interpretation is:

Find the equation of the line that passes through the 
points (0,600) and (1,545)

Slope formula:

m = 

where (x1,y1) = (0,600)
and where (x2,y2) = (1,545)

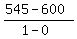m = 

m =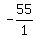 

m = -55

Point-slope formula:

y - y1 = m(x - x1)

where (x1,y1) = (0,600) and m = -55

y - 600 = -55(x - 0)

y - 600 = -55x 

y = -55x + 600

Plug in 3.5 years for x, solve for y dollars:

y = -55(3.5) + 600
y = $407.50

Plug in 0 dollars for y, solve for x years.

0 = -55x + 600
55x = 600
  x = 600/55 = 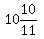 years.

Edwin