SOLUTION: three men A B C working together can do a job in 6 hrs less time than A alone, in 1 hr less time than B alone and in one half the time needed by C when working alone. then A and B

Click here to see ALL problems on Rate-of-work-word-problems

Question 958982: three men A B C working together can do a job in 6 hrs less time than A alone, in 1 hr less time than B alone and in one half the time needed by C when working alone. then A and B together can do a job in ____ minutes.
Found 2 solutions by josgarithmetic, Edwin McCravy:
Answer by josgarithmetic(39617) (Show Source):
You can put this solution on YOUR website!
Let a, b, c, be the times for each to do 1 job if each alone.

Three equations in three unknown variables. The question is to find the reciprocal of .

Could you try using the last equation to eliminate c, and have or make a simpler system? I have not worked through this; only setup the system.

Answer by Edwin McCravy(20056) (Show Source):
You can put this solution on YOUR website!
three men A B C working together can do a job in 6 hrs less time than A alone, in 1 hr less time than B alone and in one half the time needed by C when working alone. then A and B together can do a job in.

Let x = the number of hours it takes A to do 1 job working alone. Let y = the number of hours it takes B to do 1 job working alone. Let z = the number of hours it takes C to do 1 job working alone. Let t = the number of hours it takes A,B, and C to do 1 job working together. Then

three men A B C working together can do a job in 6 hrs less time than A alone,

t = x - 6 (1) x = t + 6

in 1 hr less time than B alone

t = y - 1 (2) y = t + 1

and in one half the time needed by C when working alone.

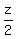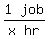
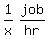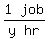
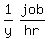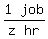
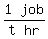
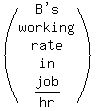
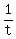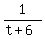
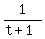
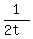
t = 2t = z (3) z = 2t A's working rate = B's working rate = C's working rate = The combined working rate of all three working together = (4) Substituting from (1), (2), and (3) into (4) 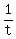Multiply through by the LCD, and get t = hour, after dicarding the negative value for t. Substituting in (1), (2), and (3) we get that A can do 1 job in 20/3 hours. B can do 1 job in 5/3 hours. C can do 1 job in 4/3 hours. But that's not what we are asked to find. What we are asked to find is given by this sentence:

A and B together can do a job in ____ hours.

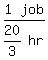
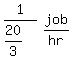
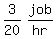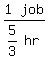
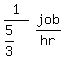
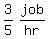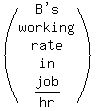
A's working rate = B's working rate = Suppose it takes them h hours to complete the job. Then The combined working rate of A&B working together = Multiply through by an LCD, solve and get h = 4/3 hr or 1 hour and 20 minutes. Edwin