SOLUTION: Describe the end behavior of the functions? I have two functions: f(x)=-x^5+3x^3-2 and f(x)=x^4-3x^2+x-1 I was wondering how to find the end behavior of each function.

Just follow these rules:

Look only at the leading term (the term with the largest exponent):

1. If its coefficient is POSITIVE --- UP on the RIGHT
2. If its coefficient is NEGATIVE --- DOWN on the RIGHT
3. If its exponent is EVEN -- LEFT hand behavior is 
the SAME as that of the RIGHT hand behavior.
4. If its exponent is ODD -- LEFT hand behavior is 
OPPOSITE to that of the RIGHT hand behavior.

Look only a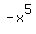t 
The leading coefficient is NEGATIVE -- DOWN on the RIGHT.
The degree is odd -- UP on the LEFT



f(x)=x^4-3x^2+x-1

Look only at 
The leading coefficient is POSITIVE -- UP on the RIGHT.
The degree is EVEN -- UP on the LEFT.



Edwin