Question 955490: A man is hauling a box of mass 100 kg up a 35º incline by a rope attached to the
top of the box. If the rope makes an angle of 20º to the incline and
the coefficient of friction between the box and the incline is 0.65, calculate the
force applied by the man to keep the box moving at constant speed.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! CORRECTED ANSWER:
Here is a representation of the situation:
(I would assume that the box is uniformly dense, and would attach the rope to the middle of the side of the box that is facing up)
 The force The force 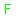 applied to make the box move uphill is represented by the green arrow. applied to make the box move uphill is represented by the green arrow.
The force of friction 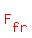 opposing the movement is represented by the red arrow. opposing the movement is represented by the red arrow.
The weight of the box is represented by the black downwards arrow.
The weight of the box,  , can be decomposed into , can be decomposed into
 , a "normal" component, perpendicular to the surface of the incline , a "normal" component, perpendicular to the surface of the incline
(here normal means perpendicular), and
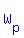 , a component parallel to the surface of the incline. , a component parallel to the surface of the incline.
Those components of the weight are represented in blue.
The red arrow for the friction force is not drawn to scale for a good reason.
I assume that the forces are all expected to be measured in Newtons,
and that we can use 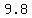 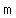 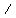 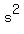 for the acceleration of gravity. for the acceleration of gravity.
That would make the magnitude of the weight (in Newtons)
 . .
The magnitudes of all the other forces will be related to  by some factor. by some factor.
The incline makes a 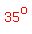 angle with the a horizontal surface (real or imaginary), angle with the a horizontal surface (real or imaginary),
so the normal weight component 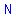 makes a makes a 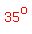 angle with the vertical weight angle with the vertical weight  . .
(It's thew same angle rotated by  and shifted). and shifted).
The blue right triangles shown in the decomposition of  tell us that tell us that
 and and
 . .
The force of friction is  times times 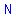 , so , so
 . .
We do not have to worry about 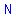 any longer, because unless the box is sinking on a soft surface, the surface is applying an opposing force that "neutralizes" any longer, because unless the box is sinking on a soft surface, the surface is applying an opposing force that "neutralizes" 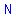 . .
As the box is moving at a constant speed, the sum of the other forces is zero,
so the magnitude of uphill-pointing 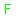 is is
the sum of the magnitudes of downhill-pointing 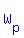 and and 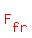 . .
The approximate value of the magnitude of the force applied by the man is
  . .
I would not use any more significant digits for the result,
because I am using a generic  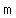 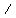 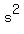 , ,
 varies with latitude, from varies with latitude, from 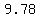 at the Equator to at the Equator to 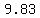 at the pole, at the pole,
and I do not know where the man and the box are.
NOTE: If I had drawn to scale the red arrow for , ,
it would have been about the same size as the blue arrow for
 , ,
and that would have made both superimposed arrows hard to see.
|
|
|