Question 954729: Given that A(0, 0), B(4, 0), C(0, 2), D(0, 0), E(12, 0), and F(0, 6), which of the following proves that ΔABC ~ ΔDEF?
A. http://my.thinkwell.com/questionbank/97001-98000/97647/img/244855.gif
B. http://my.thinkwell.com/questionbank/97001-98000/97647/img/244856.gif
C. http://my.thinkwell.com/questionbank/97001-98000/97647/img/244844.gif
D. ΔABC and ΔDEF are not similar.
Found 2 solutions by Fombitz, MathLover1:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
first find out what is the distance between given points A( , ,  ), B( ), B( , ,  ), C( ), C( , ,  )(vertices of a triangle )(vertices of a triangle  ) )
and the distance between given points D( , ,  ), E( ), E( , ,  ), and F( ), and F( , ,  ) (vertices of a triangle ) (vertices of a triangle  ) )
these distances are the lengths of the sides
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (0, 0), we can say (x1, y1) = (0, 0)
So  , , 
Since the second point is (4, 0), we can also say (x2, y2) = (4, 0)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (0, 0) and (4, 0)

 Plug in Plug in  , ,  , ,  , and , and 




==========================================================
Answer:
The distance between the two points (0, 0) and (4, 0) is exactly 4 units
|
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (0, 0), we can say (x1, y1) = (0, 0)
So  , , 
Since the second point is (0, 2), we can also say (x2, y2) = (0, 2)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (0, 0) and (0, 2)

 Plug in Plug in  , ,  , ,  , and , and 




==========================================================
Answer:
The distance between the two points (0, 0) and (0, 2) is exactly 2 units
|
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (4, 0), we can say (x1, y1) = (4, 0)
So  , , 
Since the second point is (0, 2), we can also say (x2, y2) = (0, 2)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (4, 0) and (0, 2)

 Plug in Plug in  , ,  , ,  , and , and 







==========================================================
Answer:
The distance between the two points (4, 0) and (0, 2) is exactly 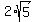 units units
The approximate distance between the two points is about 4.47213595499958 units
So again,
Exact Distance: 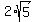 units units
Approximate Distance: 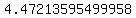 units units
|
and
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (0, 0), we can say (x1, y1) = (0, 0)
So  , , 
Since the second point is (12, 0), we can also say (x2, y2) = (12, 0)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (0, 0) and (12, 0)

 Plug in Plug in  , ,  , ,  , and , and 




==========================================================
Answer:
The distance between the two points (0, 0) and (12, 0) is exactly 12 units
|
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (0, 0), we can say (x1, y1) = (0, 0)
So  , , 
Since the second point is (0, 6), we can also say (x2, y2) = (0, 6)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (0, 0) and (0, 6)

 Plug in Plug in  , ,  , ,  , and , and 




==========================================================
Answer:
The distance between the two points (0, 0) and (0, 6) is exactly 6 units
|
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (12, 0), we can say (x1, y1) = (12, 0)
So  , , 
Since the second point is (0, 6), we can also say (x2, y2) = (0, 6)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (12, 0) and (0, 6)

 Plug in Plug in  , ,  , ,  , and , and 







==========================================================
Answer:
The distance between the two points (12, 0) and (0, 6) is exactly 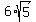 units units
The approximate distance between the two points is about 13.4164078649987 units
So again,
Exact Distance: 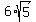 units units
Approximate Distance: 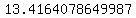 units units
|
A. http://my.thinkwell.com/questionbank/97001-98000/97647/img/244855.gif






therefore 
check:



so, the statement  is true and therefore triangle is true and therefore triangle  ~ to triangle ~ to triangle 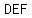 by by 
B. http://my.thinkwell.com/questionbank/97001-98000/97647/img/244856.gif
this image shows that






which is not true for given points
so, this is  an answer an answer
C. http://my.thinkwell.com/questionbank/97001-98000/97647/img/244844.gif
this image shows that by the distance formula


and also


which is  true, this is true, this is  an answer either an answer either
so, your answer is: 
|
|
|