|
Question 953872: Drains a, b, and c are used to empty a pool. drain a can empty the pool twice as fast as drain b. drain c can empty the pool 2 hours faster than drain a. working together, the three drains can empty the pool in 6 hours. how fast could drain b empty the pool working alone?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! : Drains a, b, and c are used to empty a pool. drain a can empty the pool twice as fast as drain b. drain c can empty the pool 2 hours faster than drain a. working together, the three drains can empty the pool in 6 hours. how fast could drain b empty the pool working alone?
:
let the drain times of each be a, b, c
write an equation for each statement
:
" drain a can empty the pool twice as fast as drain b.". therefore:
b = 2a
:
" drain c can empty the pool 2 hours faster than drain a." therefore:
c =(a-2)
:
working together, the three drains can empty the pool in 6 hours.
let the completed job = 1 (an empty pool)
:
 + +  + + 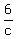 = 1 = 1
replace b with 2a and c with (a-2)
 + + 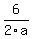 + + 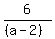 = 1 = 1
reduce the 2nd fraction
 + + 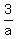 + + 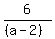 = 1 = 1
multiply by a(a-2), cancel the denominators and you have:
6(a-2) + 3(a-2) + 6a = a(a-2)
6a - 12 + 3a - 6 + 6a = a^2 - 2a
Combine like terms
15a - 18 = a^2 - 2a
Combine on the right to form a quadratic equation
0 = a^2 - 2a - 15a + 18
a^2 - 17a + 18 = 0
we have to use the quadratic formula to solve this; a=1, b=-17, c=18
I got inexact solutions, a = 15.865 is the reasonable answer
a = 15.865 hrs alone
:
how fast could drain b empty the pool working alone?
Takes twice as long, therefore
2*15.865 = 31.73 hrs
:
:
let's check this; c=13.865 (two hrs less)
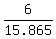 + + 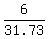 + + 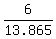 = =
.378 + .189 + .433 = 1, this is a good solution
|
|
|
| |