Question 953766: Please help me solve this equation:
There are 45 multiple-choice questions, each of 4 choices. Only one of them is correct. Suppose a student picks all the choices randomly. What is the probability of him getting at least 40 questions correct?
Thank you!!!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the probability is very close to 0 that he will get at least 40 questions correct.
see the following picture:
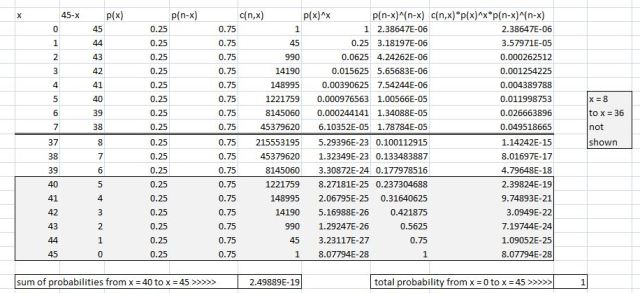
the total probability is 1 as it should be.
the probability from x = 40 to x = 45 is equal to 2.49889E-19.
that's 2.49889 * 10^-19.
it's so small that it is effectively 0.
you use the binomial theorem.
that theorem states:
p(x) = c(n,x) * p^x * q^(n-x)
to find the probability of getting more then or equal to 40 right, you need to take the sum of p(x) from x = 40 to x = 45.
that's what is shown in the picture.
one of those calculations would be done as follows:
p(40) = c(45,40) * .25^40 * .75^5.
c(45,40) is equal to 1221759
.25^40 is equal to 7,26179513... * 10^-25
.75^5 is equal to .2373046875
c(45,40) is the number of possible ways you can get 40 items out of 45 if you don't take order into account. That's the combination formula of C(n,x) = n! / (x! * (n-x)!)
c(45,40) * .25^40 * .75^5 is equal to 2.39823762 * 10^-19
the picture for x = 40 is showing you a probability of 2.39824E-19.
that's the probability of getting exactly 40 right out of the 45 questions/.
the picture value is rounded more than the calculated value.
that's the only difference.
they are the same.
the same formula is applied for x = {41, 42, 43, 44, 45} and then all of the probabilities from x = 40 to x = 45 are added up to get the probability of x being greater than or equal to 40.
it's a very small number that is, for all practical purposes, equal to 0.
|
|
|