Question 953542: The function f is a fifth-degree polynomial with
the x-intercepts -4, 1, and 7,
y-intercept 112 and
f (x) ≥ 0 for x ≤ 7
I know it would have to have (x+4)(x-1)(x+7) and possibly either squared or cubics for exponents but I am confused about how I would insert the 112 and the f (x) ≥ 0 for x ≤ 7. I don't understand what those last two are asking me to do to make it true.
Thanks
Found 2 solutions by MathLover1, ankor@dixie-net.com:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
a fifth-degree polynomial with
the x-intercepts  , ,  , and , and  , ,
y-intercept  and and
 for for 
By hypothesis,  has factors has factors  , ,  , and , and by the Factor Theorem. by the Factor Theorem.
==>  for some 2nd degree polynomial for some 2nd degree polynomial  . .
To determine  : :
We need  for for  . .
==>  for for 
Note that each factor is negative for some  . .
There a few ways to deal with this; here is one way.
Note that both 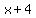 and and 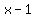 change signs when change signs when  , while , while  does not. does not.
Since we need  to be quadratic, we can take to be quadratic, we can take  for some constant for some constant  . .
Now, we have  for some for some  . .
Note: that we have not changed the x-intercepts by repeating some of the factors
Since  is never negative, needing is never negative, needing  for for  reduces to needing reduces to needing  for for  . .
*This is guaranteed if 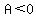 . .
Finally, we use  to determine to determine  : :




==> , which is indeed negative. , which is indeed negative.
Hence, we can take



Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The function f is a fifth-degree polynomial with
the x-intercepts -4, 1, and 7,
y-intercept 112 and
f (x) ≥ 0 for x ≤ 7
:
We have the three factors (x+4)(x-1)(x-7), the y intercept 4 * 1 * 7 = 28 not 112.
28 goes into 112 4 times so lets change the factors to (x+4)(x-1)(4x-28)
4x + 28 = 0; x still equal -7
but now we can construct the equation
FOIL(x+4)(x-1) = x^2 + 3x - 4
:
x^2 + 3x - 4
X (4x - 28)
-------------
4x^3 - 16x^2 - 100x + 112 but this only a third degree equation but satisfies the requirements

Green line is y=112
|
|
|