Question 953541: The function p is a fourth-degree polynomial with x-intercepts 0.5, 5, and 10 and y-intercept -1. If p(x) is positive only on the interval (5, 10), find p(x).
How would I go about solving?
Thank you
Found 2 solutions by stanbon, MathLover1:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! The function p is a fourth-degree polynomial with x-intercepts 0.5, 5, and 10 and y-intercept -1. If p(x) is positive only on the interval (5, 10), find p(x).
How would I go about solving?
---------
Given those x-intercepts you get::
y = a(2x-1)(x-5)
----
With the y-intercept you can solve for "a":
10 = a(-1)(-5)
a = 2
-----
Equation:
y = 2(2x-1)(x-5)
-----
Note:: Being a quadratic it cannot be positive on (5,10) if it has
x intercepts 0.5 and 5.
Cheers,
Stan H.
========
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The function  is a fourth-degree polynomial with x-intercepts is a fourth-degree polynomial with x-intercepts 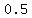 , ,  , and , and  and y-intercept and y-intercept  . .
If 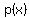 is positive only on the interval ( is positive only on the interval ( , ,  ), find ), find 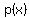 . .
A fourth-degree polynomial must have  roots. roots.  are given. Presumably are given. Presumably 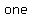 of those three has multiplicity of of those three has multiplicity of  , as opposed to there being an entirely separate root that the problem isn't telling about. , as opposed to there being an entirely separate root that the problem isn't telling about.
 and and  can't either have a multiplicity of can't either have a multiplicity of  without violating the condition about "positive only on the interval ( without violating the condition about "positive only on the interval ( , ,  )", so that leaves )", so that leaves 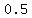 or or  to be the multiple root. to be the multiple root.
Use the factor theorem to convert the four roots into factors:

Multiply these factors together:

The y-intercept of this function is 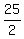 , so to achieve the desired y-intercept, multiply all the coefficients by , so to achieve the desired y-intercept, multiply all the coefficients by  : :




as you can see on a graph,
x-intercepts are 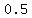 , ,  , and , and 
y-intercept is  , ,
and
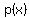 is positive only on the interval ( is positive only on the interval ( , ,  ) )
|
|
|