Question 951215: Please help !
Jane leaves her house and drives in a straight line at a speed of 50 mph. Her speed on the return trip is 60 mph. The trip back home takes 20 minutes less than the outbound trip. What was Jane's total travel time in hours? Assume both trips are in a straight line. Give your final answer as a simplified fractio
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! It is good to be able to solve a problem two different ways so as to confirm one answer with the other.
THE FIFTH GRADER says.
Let's imagine Jane drove 50 miles away from home,
and then turned around and drove the 50 miles back home.
If the one-way distance was 50 miles, she would have made the trip away from home in 1 hour (60 minutes),
and since 60 miles per hour is 1 mile per minute,
the 50-mile trip back home would have taken 50 minutes,
which is 10 minutes shorter,
and the round trip would take a total of 110 minutes (60+50=110).
So, as Jane's return was 20 minutes rather than 10 minutes shorter than her trip away from home (twice as long),
the distances and times must be double what we imagined.
So jane drove 100 miles and the round trip took her 220 minutes (twice 110 minutes).
The problem does not tell you what units are required.
Do they expect the answer in hours?
Probably, because they talk about fractions.
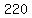 minutes, in hours, is minutes, in hours, is  hours. hours.
(We could always say 3 hours and 20 minutes, which sounds more like real life).
ANOTHER WAY TO THE SOLUTION THAT USES ALGEBRA:
First, we define a variable, in a way that we hope makes the calculations simpler.
 = time (hours) that Jane spent driving away from home. = time (hours) that Jane spent driving away from home.
(Use  if you prefer). if you prefer).
   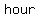 , so , so
 = distance (miles) that Jane drove away from home = distance (miles) that Jane drove away from home
(how far from home Jane was when she turned around).
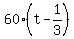 = distance (miles) that Jane drove going back home. = distance (miles) that Jane drove going back home.
They are the same distance, so
 is our equation. is our equation.
Solving:








So the whole trip took  hours. hours.
The time (in hours for the round trip was (substituting  ) )
 . .
|
|
|