Question 950377: Please help me solve this, I know there is a calculation that can be done, but don't know what that is.
how many subsets and proper subsets are there fir {t,e,j,a,n,i,g,l}?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! subsets and proper subsets are there fir {t,e,j,a,n,i,g,l}
Recall, the number of subsets for set  is is 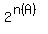 where where 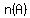 is the number of elements in set is the number of elements in set  . .
in your case  , so you will have , so you will have  subsets subsets
recall that the empty set is a proper subset of any nonempty set
recall that {a, b} is a proper subset of {a, b, c}, but {a, b, c} is not a proper subset of {a, b, c}
so, in your case there is 
all subsets and proper subsets of {t,e,j,a,n,i,g,l}:
{},{t},{e},{j},{a},{n},{i},{g},{l},{t,e},{t,j},{t,a},{t,n},{t,i},{t,g},{t,l},{e,j},{e,a},{e,n},{e,i},{e,g},{e,l},{j,a},{j,n},{j,i},{j,g},{j,l},{a,n},{a,i},{a,g},{a,l},{n,i},{n,g},{n,l},{i,g},{i,l},{g,l},{t,e,j},{t,e,a},{t,e,n},{t,e,i},{t,e,g},{t,e,l},{t,j,a},{t,j,n},{t,j,i},{t,j,g},{t,j,l},{t,a,n},{t,a,i},{t,a,g},{t,a,l},{t,n,i},{t,n,g},{t,n,l},{t,i,g},{t,i,l},{t,g,l},{e,j,a},{e,j,n},{e,j,i},{e,j,g},{e,j,l},{e,a,n},{e,a,i},{e,a,g},{e,a,l},{e,n,i},{e,n,g},{e,n,l},{e,i,g},{e,i,l},{e,g,l},{j,a,n},{j,a,i},{j,a,g},{j,a,l},{j,n,i},{j,n,g},{j,n,l},{j,i,g},{j,i,l},{j,g,l},{a,n,i},{a,n,g},{a,n,l},{a,i,g},{a,i,l},{a,g,l},{n,i,g},{n,i,l},{n,g,l},{i,g,l},{t,e,j,a},{t,e,j,n},{t,e,j,i},{t,e,j,g},{t,e,j,l},{t,e,a,n},{t,e,a,i},{t,e,a,g},{t,e,a,l},{t,e,n,i},{t,e,n,g},{t,e,n,l},{t,e,i,g},{t,e,i,l},{t,e,g,l},{t,j,a,n},{t,j,a,i},{t,j,a,g},{t,j,a,l},{t,j,n,i},{t,j,n,g},{t,j,n,l},{t,j,i,g},{t,j,i,l},{t,j,g,l},{t,a,n,i},{t,a,n,g},{t,a,n,l},{t,a,i,g},{t,a,i,l},{t,a,g,l},{t,n,i,g},{t,n,i,l},{t,n,g,l},{t,i,g,l},{e,j,a,n},{e,j,a,i},{e,j,a,g},{e,j,a,l},{e,j,n,i},{e,j,n,g},{e,j,n,l},{e,j,i,g},{e,j,i,l},{e,j,g,l},{e,a,n,i},{e,a,n,g},{e,a,n,l},{e,a,i,g},{e,a,i,l},{e,a,g,l},{e,n,i,g},{e,n,i,l},{e,n,g,l},{e,i,g,l},{j,a,n,i},{j,a,n,g},{j,a,n,l},{j,a,i,g},{j,a,i,l},{j,a,g,l},{j,n,i,g},{j,n,i,l},{j,n,g,l},{j,i,g,l},{a,n,i,g},{a,n,i,l},{a,n,g,l},{a,i,g,l},{n,i,g,l},{t,e,j,a,n},{t,e,j,a,i},{t,e,j,a,g},{t,e,j,a,l},{t,e,j,n,i},{t,e,j,n,g},{t,e,j,n,l},{t,e,j,i,g},{t,e,j,i,l},{t,e,j,g,l},{t,e,a,n,i},{t,e,a,n,g},{t,e,a,n,l},{t,e,a,i,g},{t,e,a,i,l},{t,e,a,g,l},{t,e,n,i,g},{t,e,n,i,l},{t,e,n,g,l},{t,e,i,g,l},{t,j,a,n,i},{t,j,a,n,g},{t,j,a,n,l},{t,j,a,i,g},{t,j,a,i,l},{t,j,a,g,l},{t,j,n,i,g},{t,j,n,i,l},{t,j,n,g,l},{t,j,i,g,l},{t,a,n,i,g},{t,a,n,i,l},{t,a,n,g,l},{t,a,i,g,l},{t,n,i,g,l},{e,j,a,n,i},{e,j,a,n,g},{e,j,a,n,l},{e,j,a,i,g},{e,j,a,i,l},{e,j,a,g,l},{e,j,n,i,g},{e,j,n,i,l},{e,j,n,g,l},{e,j,i,g,l},{e,a,n,i,g},{e,a,n,i,l},{e,a,n,g,l},{e,a,i,g,l},{e,n,i,g,l},{j,a,n,i,g},{j,a,n,i,l},{j,a,n,g,l},{j,a,i,g,l},{j,n,i,g,l},{a,n,i,g,l},{t,e,j,a,n,i},{t,e,j,a,n,g},{t,e,j,a,n,l},{t,e,j,a,i,g},{t,e,j,a,i,l},{t,e,j,a,g,l},{t,e,j,n,i,g},{t,e,j,n,i,l},{t,e,j,n,g,l},{t,e,j,i,g,l},{t,e,a,n,i,g},{t,e,a,n,i,l},{t,e,a,n,g,l},{t,e,a,i,g,l},{t,e,n,i,g,l},{t,j,a,n,i,g},{t,j,a,n,i,l},{t,j,a,n,g,l},{t,j,a,i,g,l},{t,j,n,i,g,l},{t,a,n,i,g,l},{e,j,a,n,i,g},{e,j,a,n,i,l},{e,j,a,n,g,l},{e,j,a,i,g,l},{e,j,n,i,g,l},{e,a,n,i,g,l},{j,a,n,i,g,l},{t,e,j,a,n,i,g},{t,e,j,a,n,i,l},{t,e,j,a,n,g,l},{t,e,j,a,i,g,l},{t,e,j,n,i,g,l},{t,e,a,n,i,g,l},{t,j,a,n,i,g,l},{e,j,a,n,i,g,l},{t,e,j,a,n,i,g,l}
|
|
|