Question 949880: Terrell drove to the mountains at an average 60mph. His return trip, by the same roads, averaged 40mph. His total driving time was 12 hours. How far did he drive one way?
Found 2 solutions by macston, MathTherapy:
Answer by macston(5194)   (Show Source): (Show Source):
You can put this solution on YOUR website! d=distance one way; t=time; r1=rate going; r2=rate returning
t=d/r1+d/r2=d/60mph+d/40mph=d(1/60mph+1/40mph)
t=1/60+1/40=2/120+3/120=5/120=d(1/24 mph)multiply each side by 24 mph.
t*24 mi/hr=d
12 hrs(24 mi/hr)=d
288 mi=d ANSWER: Terrell drove 288 miles one way
CHECK:
round trip=12 hrs
12 hrs=288 mi/60 mph+288 mi/40 mph=4.8 hrs+7.2 hrs
12 hrs=12 hrs
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Terrell drove to the mountains at an average 60mph. His return trip, by the same roads, averaged 40mph. His total driving time was 12 hours. How far did he drive one way?
Let distance one-way, be D
Then time taken on outbound trip = 
Time taken on inbound trip = 
Since total time was 12 hours, we get: 
2D + 3D = 1,440 -------- Multiplying by LCD, 120
5D = 1,440
D, or distance, one way = 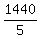 , or , or  miles miles
|
|
|