|
Question 949859: Could someone explain what reflecting means? I keep hearing about reflecting in the x-axis and reflecting in the y-axis. What is reflecting? Is this taking the mirror image of whatever it is? But then my question becomes what does it mean by reflecting in the x or y axis? AM I REALLY CONFUSED
Found 3 solutions by richard1234, stanbon, MathLover1:
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! "What is reflecting? Is this taking the mirror image of whatever it is?"
Essentially. Think about looking at yourself in a mirror.
We usually say "reflect about the x- (or y-) axis." For example, the point (1,5) reflected about the x-axis maps to (1,-5).
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! Could someone explain what reflecting means? I keep hearing about reflecting in the x-axis and reflecting in the y-axis. What is reflecting? Is this taking the mirror image of whatever it is? But then my question becomes what does it mean by reflecting in the x or y axis?
--------
Reflecting in the y-axis.
Example:: Start with (2,3)
Draw a perpendicular to the y-axis to (0,3)
Go an equal distance to the other side of the y-axis
to (-2,3)
That is the point of reflection of (2,3) in the y-axis.
-----
Reflecting in the x-axis.
Example:: Start with (2,3)
Draw a perpendicular to the x-axis to (2,0)
Go an equal distance to the other side of the x-axis
to (2,-3)
That is the point of reflection of (2,3) in the x-axis.
--------------
Cheers,
Stan H.
---------------
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website! A reflection is a kind of transformation. It is basically a 'flip' of a shape over the line of reflection. Very often reflections are performed using coordinate notation because it allow us to easily describe the image and its pre-image.
Reflection in the  -axis.
A reflection in the x-axis when 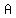 is reflected to its image  ' or  then point (, ) -> (,  )
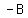let it be points ( , ) -> (, )
to remember it easier you just imagine x-axis is a mirror, point (,) is like you standing in front of that mirror and you see your reflection in mirror, same is with a point (,) whose reflection is (, )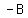
A reflection in the y-axis when is reflected to its image ' or then point (,) -> ( , )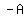
using a point ( , ) , we have
A reflection in the line  when is reflected to its image then point (,) -> (, )
if we use same point (,) , we have
|
|
|
| |
