|
Question 949683: Please help me find the vertex and the directrix of the following parabola : 9(x-1)^2=36(y+2)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  <---> <---> is the equation of a parabola is the equation of a parabola
with axis of symmetry  >---> >---> . .
That is easy to see even if you know nothing about parabolas.
You do not need to know anything about parabolas to realize that the equation
gives the same value to 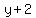 when when  and when and when  . .
Generalizing, we would say that 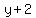 has the same value has the same value
when  is a distance is a distance 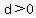 to the right of to the right of  (when (when  ), ),
as when  is a distance is a distance 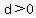 to the left of to the left of  (when (when  <--> <--> ). ).
We know that  . .
For  <---> <---> , ,
 and and  , ,
so for   <---> <---> . .
For  <---> <---> , ,
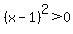 and and  , ,
so for   <---> <--->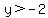 . .
To either side of  the value for the value for  is greater than for is greater than for  . .
That tells us that  (for (for  ) is the minimum of the graph, ) is the minimum of the graph,
and that the point (1,-2) is the vertex of the parabola.
Finding the directrix requires knowing a bit about parabolas.
Maybe you remember (or finding in your textbook) a definition that says that a parabola is the set of points on a plane, such that
the distance from the vertex to the focus and
the distance from the vertex to a line called the directrix are the same.
From that definition, with a little algebra knowledge, and a lot of thinking,
you could get all you need to know about parabolas
(unless they ask you what is the "latus rectum" ).
Most people just read on until they find a formula that they can apply to the problem, whether they understand why it is so or not.
Many try to memorize that formula and remember it,
at least until they take the test on parabolas.
However, just from the definition of parabola,
you could get to the conclusion that
1) the equation for any parabola with a horizontal directrix,
and a vertex at the origin can be written as
 ; ;
2) the focus is at (0,1/4a) ( 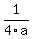 above the vertex), and above the vertex), and
3) the directrix is the line  , , 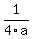 below the vertex. below the vertex.
If the vertex were instead the point (h,k),
the formula would be  , ,
but the rest would be the same.
Your equation,  , ,
looks like  , ,
with  , ,
so the vertex, (h,k), is (1,-2),
and the directrix is  below the vertex. below the vertex.
So the directrix is the horizontal line with
 , ,
 . .
Here is what the parabola and directrix look like:

|
|
|
| |