Question 949343: Hi!
I have been trying to solve this problem quite a while, and help for solving this would be great.
In a strict monarchy there are 100 monks, either senior or junior. If a senior monk is allowed to have 3 slices of break for each meal, and a junior monk is only allowed 1/3 of a slice, and altogether the consume 60 slices of break during lunch, how many senior monks are there?
I know that the answer is 10, but I was just wondering how it is possible to come to that answer.
Thank you!
Found 2 solutions by macston, MathTherapy:
Answer by macston(5194)   (Show Source): (Show Source):
You can put this solution on YOUR website! S=number of senior monks; J=number of junior monks
S+J=100 Subtract S from each side
J=100-S
1/3J+3S=60 Substitute for J.
1/3(100-S)+3S=60
33 1/3-1/3S+3S=60 Subtract 33 1/3 from each side.
8/3 S=26 2/3 Multiply each side by 3/8.
S=(80/3)*(3/8)=10 ANSWER: There are 10 senior monks.
CHECK:
J=100-2=90 There are 90 junior monks,
1/3J+3S=60
1/3(90)+3(10)=60
30+30=60
60=60
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi!
I have been trying to solve this problem quite a while, and help for solving this would be great.
In a strict monarchy there are 100 monks, either senior or junior. If a senior monk is allowed to have 3 slices of break for each meal, and a junior monk is only allowed 1/3 of a slice, and altogether the consume 60 slices of break during lunch, how many senior monks are there?
I know that the answer is 10, but I was just wondering how it is possible to come to that answer.
Thank you!
You must be referring to BREAD here, and not BREAK
Let number of senior monks be S
Then number of junior monks = 100 – S
We then get: 

9S + 100 – S = 180 ---------- Multiplying by LCD, 3
9S – S = 180 – 100
8S = 80
S, or number of senior monks = 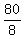 , or , or 
|
|
|