Question 949199: Suppose that the playground area has a length of x yards and a width of y yards. The only restriction on the playground is that the area must be 324 square yards.
a.In terms of x and y, find a formula for the perimeter, P.
b.In terms of x and y, find an equation that models the area of the playground (324 square yards).
c.Combine your formula for the perimeter, P, and the equation of the area by writing a formula for the perimeter, P, in terms of x.
d.Use the formula from Part C to find the Perimeter, P, for each value of x. Include a copy of the completed table in your answer.
x
P
9
10
18
e.Among the three sets of dimensions determined by the values of x above, which set represents the playground area with the smallest perimeter?
Found 2 solutions by rothauserc, MathLover1:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) Perimeter(P) = 2x + 2y
b) 324 = xy
c) from b, y = 324/x, then
P = 2x + 2(324/x)
d) if x = 9, then
P = (2*9) + (2*(324/9))
P = 18 + 72 = 90 yards
******
if x = 10, then
P = (2*10) + (2*(324/10))
P = 20 + 64.8 = 84.8 yards
******
if x = 18, then
P = (2*18) + (2*(324/18))
P = 36 + 36 = 72 yards
******
all squares are rectangles but all rectangles are not squares, therefore
72 yards is the minimum perimeter with its sides = 18 yards
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose that the playground area has a length of  yards and a width of yards and a width of  yards. The only restriction on the playground is that the area must be yards. The only restriction on the playground is that the area must be 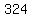 square yards. square yards.
the playground area is 
given:



a.
In terms of  and and  , find a formula for the perimeter, , find a formula for the perimeter,  . .
since  , we have , we have

b.
In terms of  and and  , find an equation that models the area of the playground (324 square yards). , find an equation that models the area of the playground (324 square yards).
since given



we have 
c.
Combine your formula for the perimeter, , and the equation of the , and the equation of the  by writing a formula for the perimeter, by writing a formula for the perimeter,  , in terms of , in terms of  . .
to do so, first use  and solve for and solve for 
 ....now substitute this in ....now substitute this in 
 => =>
d.
Use the formula from Part C to find the Perimeter,  , for each value of , for each value of . Include a copy of the completed table in your answer. . Include a copy of the completed table in your answer.
 |----- |-----
 |----- |----- -> -> -> -> -> ->
 |----- |-----  -> -> -> -> -> ->
 |----- |----- -> -> -> -> -> ->
e.
Among the three sets of dimensions determined by the values of 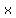 above, which set represents the playground area with the smallest perimeter? above, which set represents the playground area with the smallest perimeter?
the smallest perimeter  , so we can find , so we can find  using using






set  , , represents the playground area with the smallest perimeter represents the playground area with the smallest perimeter
|
|
|