Question 948356: Is my answer correct for this inequality?
((x+5)^2(8-x))/(x^2-16)≥0
Had to answer in interval notation
what I got was: (-∞,-4]U[4,8)
Please explain
Thanks
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  ......multiply ......multiply 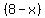 by by  to get to get 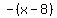 , put minus in front and do not forget, sign ≥ will become £ , put minus in front and do not forget, sign ≥ will become £


as you know, denominator cannot be equal to zero; so, we need to exclude values of  that make denominator equal to zero and they are: that make denominator equal to zero and they are:

if  => =>
if  => =>
also, we need to exclude values of  that make numerator equal to zero and they are that make numerator equal to zero and they are
 => =>
 => => 
so,since we already have excluded and => and =>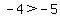 then then  will be included in interval ( will be included in interval ( , ,  ) )
so, interval notation is:
( , ,  ) U ( ) U ( , ,  ] ]

so, your solution is part of graph above x-axis, left from blue line passing through  and between blue lines passing through and between blue lines passing through  and and 
|
|
|