Question 948186: From a point, M, the angle of elevation to the top of a building, B, is 34°. From a
point, N, 20 m closer to the building, the angle of elevation is 49°.
Calculate the distance NB, correct to 1 decimal place.
help please??? ive been trying for an hour and havent even started working it out
Found 2 solutions by rothauserc, ankor@dixie-net.com:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! we can use the law of sines to solve this problem, law of sines for any triangle is
(sin(A)/a) = (sin(B)/b) = (sin(C)/c)
consider triangle NBM
angle MNB = 180 - 49 = 131
angle NBM = 180 - (131+34) = 15
therefore
(sin(15)/20) = (sin(34)/BN)
BN = (sin(34)*20) / sin(15)) = 11.183858069 / 0.258819045 = 43.211109387 and
BN = 43.2 m
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! From a point, M, the angle of elevation to the top of a building, B, is 34°. From a point, N, 20 m closer to the building, the angle of elevation is 49°.
Calculate the distance NB, correct to 1 decimal place.
:
Draw this out, concentrate on the triangle M N and the top of the building
We can find the all three angles of this triangle m = 34, n: 180-49 = 131; and the angle at the top of the building: 180 - 131 - 34 = 15 degrees
Use he law of sines to find the side from M to to the top of the building.
It is also the hypotenuse of a right triangle formed by m and the building
Call that side h
 = = 
 = = 
cross multiply
.2588h = 20 * .7547
.2588h = 15.1
h = 
h = 58.32 meters from m to the top of the building
This is also the hypontenuse of the right triangle as we said before
Find the distance from m to the base of the building using the cosine of 34
Call this d
cos(34) = 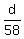
.829 = 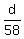
d = 58.32 * .829
d = 48.35 meters from M to the base of the building
find the distance from N to the building
48.35 - 20 = 28.35 meters
:
:
Did I make this understandable to you? Let me know. ankor@att.net
|
|
|