Question 948147: When a plane flies into the wind , it can travel 3000km in 6 hours. When it flies with the wind, it can travel the same distance in 5 hours. Find the rate of the plane in still air and the rate of the wind.
I sorta know how to do these problems. I am just a little confused on this one. Could you help me with this one please?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! RT=D rate time distance
VARIABLES
r, speed if no wind
w, speed of wind
u, time in a direction of travel
v, time in the opposite direction of travel
d, distance one way or either way for the trip
-
u=6
v=5
d=3000
-
Unknown variables for which to solve are r and w.
Related to wind__________rate___________time___________distance
AGAINST__________________r-w______________u______________d
WITH_____________________r+w______________v______________d
System of equations before refinements:

Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
When a plane flies into the wind , it can travel 3000km in 6 hours. When it flies with the wind, it can travel the same distance in 5 hours. Find the rate of the plane in still air and the rate of the wind.
I sorta know how to do these problems. I am just a little confused on this one. Could you help me with this one please?
Let speed of plane in still air, be S, and speed of wind, W
Average speed when flying against wind: 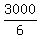 , or 500 km , or 500 km
Average speed when flying with wind: 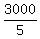 , or 600 km , or 600 km
Speed of plane in still air, less wind’s speed, equals average speed against wind, OR
S – W = 500 -------- eq (i)
Speed of plane in still air, plus wind’s speed, equals average speed with wind, OR
S + W = 600 -------- eq (ii)
2S = 1,100 -------- Adding eqs (ii) & (i)
S, or speed of plane in still air = 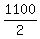 , or , or  km/h km/h
550 – W = 500 -------- Substituting 550 for S in eq (i)
- W = 500 – 550
- W = - 50
W, or speed of wind = 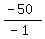 , or , or  km/h km/h
|
|
|